In questa pagina si discutono i risultati della progettazione per una trave a sbalzo in cemento armato sottoposta a flessione biassiale e a forza assiale.
| Forza assiale | \(N_{Ed}\) | \(\) | 2000 | kN |
| Momento flettente X | \(M_{Ed,X}\) | \(\) | 234 | kNm |
| Momento flettente Z | \(M_{Ed,Z}\) | \(\) | 100 | kNm |
Puoi trovare il modello in WeStatiX pronto per il tuo calcolo.
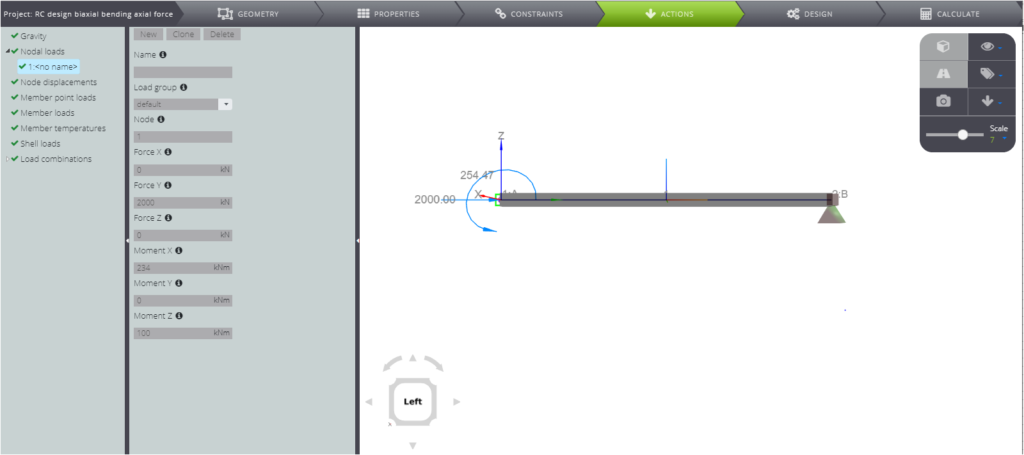
Nella tabella sottostante sono riportati i parametri della sezione trasversale
| DESCRIZIONE | SIMBOLO | VALORE | UM | |
|---|---|---|---|---|
| Larghezza complessiva di una sezione trasversale | \(b\) | \(\) | 300 | mm |
| Altezza | \(h\) | \(\) | 400 | mm |
| Copriferro superiore | \(d_1\) | \(\) | 50 | mm |
| Copriferro inferiore | \(d_2\) | \(\) | 50 | mm |
| \(d’\) | \(h-d_1\) | 350 | mm | |
| – | \(b’\) | \(b-d_2\) | 250 | mm |
| Rapporto per la scelta del diagramma di interazione | \(d’/h\) | \(\) | ,13 | – |
E i parametri del materiale
| DESCRIZIONE | SIMBOLO | VALORE | UM | |
|---|---|---|---|---|
| Resistenza caratteristica a compressione per provini cilindrici a 28 giorni | \(f_{ck}\) | \(\) | 42.500,00 | kPa |
| Resistenza caratteristica a snervamento dell’armatura | \(f_{yk}\) | \(\) | 549.700,00 | kPa |
| Coefficiente per gli effetti a lungo termine | \(\alpha_{cc}\) | \(\) | 1,00 | – |
| Coefficiente di sicurezza per il calcestruzzo | \(\gamma_c\) | \(\) | 1,50 | – |
| Coefficiente di sicurezza per l’acciaio da armatura | \(\gamma_s\) | \(\) | 1,15 | – |
| Valore di progettazione per la resistenza a compressione del calcestruzzo | \(f_{cd}\) | \(\alpha_{cc} f_{ck}/\gamma_c\) | 28.333,33 | kPa |
| Valore di progettazione per la resistenza a snervamento dell’acciaio da armatura | \(f_{yd}\) | \(f_{yk}/\gamma_{s}\) | 478.000,00 | kPa |
Osservando i risultati del progetto del membro RC, l’area totale di rinforzo sarà di \(A_{s,tot}=29,02 cm^2\).
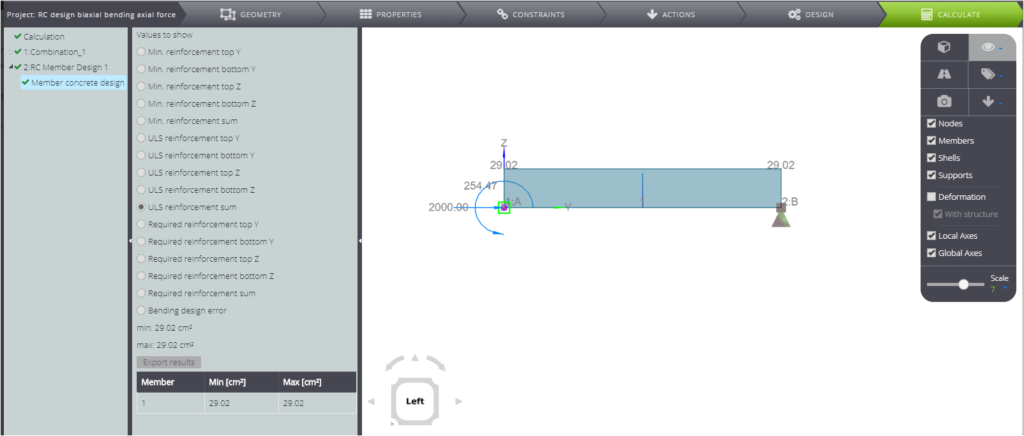
Potete verificare utilizzando i diagrammi di interazione come suggerito in [1]. In base a ciò, occorre trovare i seguenti parametri
| \(\beta\) | \(1-N_d/b \cdot h \cdot f_{ck}\) | 0,61 | – | |
| Momento effettivo monoassiale | \(M’_z\) | \(M_x+\beta M_y d/b’ \) | 322,64 | kNm |
| Forza assiale parametrizzata | \(\nu\) | \(N_d/b \cdot h \cdot f_{cd}\) | 0,59 | – |
| Momento flettente parametrizzato | \(\mu\) | \(M’_z/b\cdot h^2 \cdot f_{cd}\) | 0,24 | – |
Perciò bisogna considerare i diagrammi di interazione per il progetto per la flessione biassiale e la forza assiale per una sezione con d’/h=0,10 and d’/h=0,15, riportati di seguito
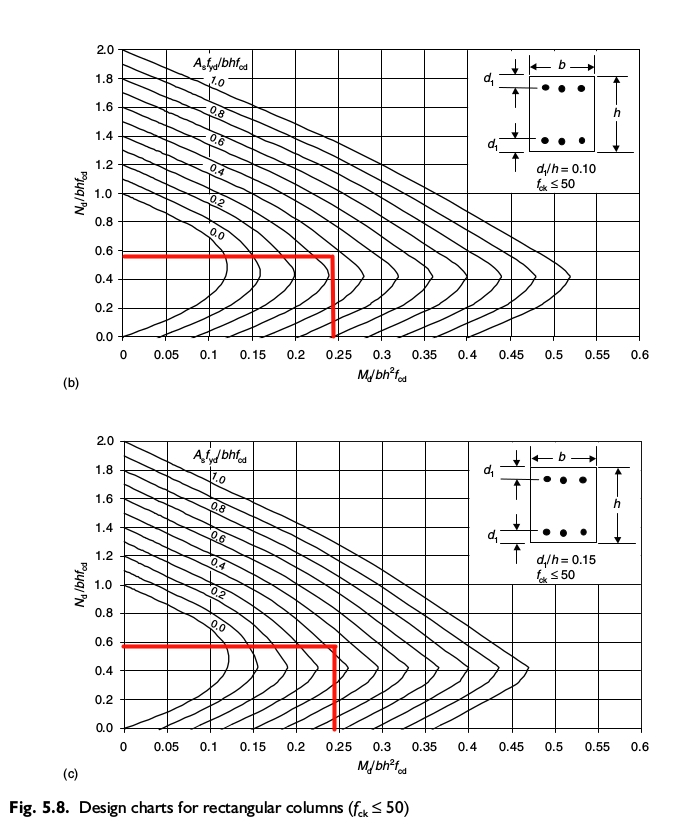
Risulta facile quindi trovare l’area totale di acciaio da armatura
| Coefficiente dal diagramma di interazione | \(A_s \cdot f_{yd} / b \cdot h \cdot f_{cd}\) | \(\) | 0,41 | – |
| Area di rinforzo totale | \(A_{s,tot}\) | \(\) | 29,16 | cm^2 |
Infine, è possibile calcolare l’errore nel modo seguente
WeStatiX soddisfa la soluzione.
[1] A.W.. BEEBY and R.S: NARAYANAN – Designers’ guide to Eurocode 2: design of concrete structures. – Designers’ guide to EN1992-1-1 and EN1992-1-2 Eurocode 2: design of concrete structures. General rules and rules for buildings and structural fire design.
