Auf dieser Seite vergleichen wir die analytische und die numerische Lösung für eine gleichmäßig belastete, an den Ecken gelagerte quadratische Platte.
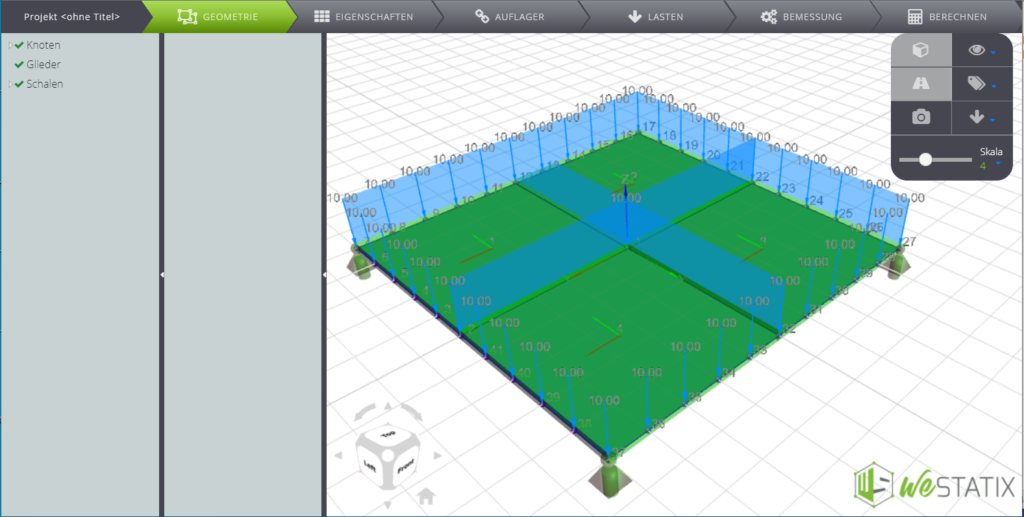
Sie können die Daten in der folgenden Tabelle lesen.
| Young’s modulus | E | 100.000.000 | kPa |
| Dicke | h | 0,30 | m |
| Poissonzahl | \(\nu\) | 0,30 | – |
| Länge | a | 10,00 | m |
| Gleichmäßiger Druck | q | -10,00 | kPa |
| Biegesteifigkeit der Platte | D | 247253,75 | kN/m |
Die Biegesteifigkeit der Platte wird als \( {E \cdot h^3}/{12(1-\nu^2)}\) berechnet.
Wenn Sie entdecken wollen, wie man das Modell baut, können Sie in unserer Dokumentation nachlesen, wie wir ein ähnliches Modell gebaut haben. Sie müssen nur die Schritte bis auf die Auflager entlang der Kanten befolgen.
Ansonsten finden Sie sie über unsere öffentlichen Tutorials in WeStatiX, wo Sie nur die Berechnung starten müssen.
Nun können Sie die Ergebnisse mit der in Theory of plates and shells [1] angegebenen Lösung vergleichen.
| BESCHREIBUNG | PARAMETER | EINH. | ANALYTISCHE LÖSUNG | WSX | FEHLER |
|---|---|---|---|---|---|
| Durchbiegung (x=0; y=0) | \(w_{max}\) | m | -1,01E-02 | -1,03E-02 | 2% |
| Biegemoment in der Mitte der Platte (x=0; y=0) | \(M_{x _{max}}\) | kNm/m | -109,00 | -108,594 | 0% |
| Biegemoment an der Kante (x=0; y=a/2) | \(M_{y _{max}}\) | kNm/m | -140,40 | -142,716 | 2% |
Schließlich können Sie hier einige Screenshots der Ergebnisse sehen.
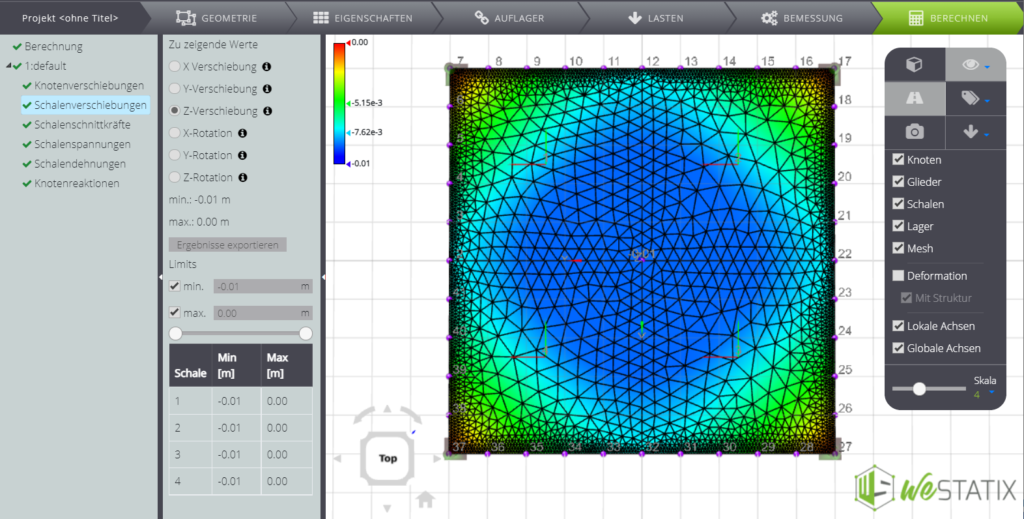
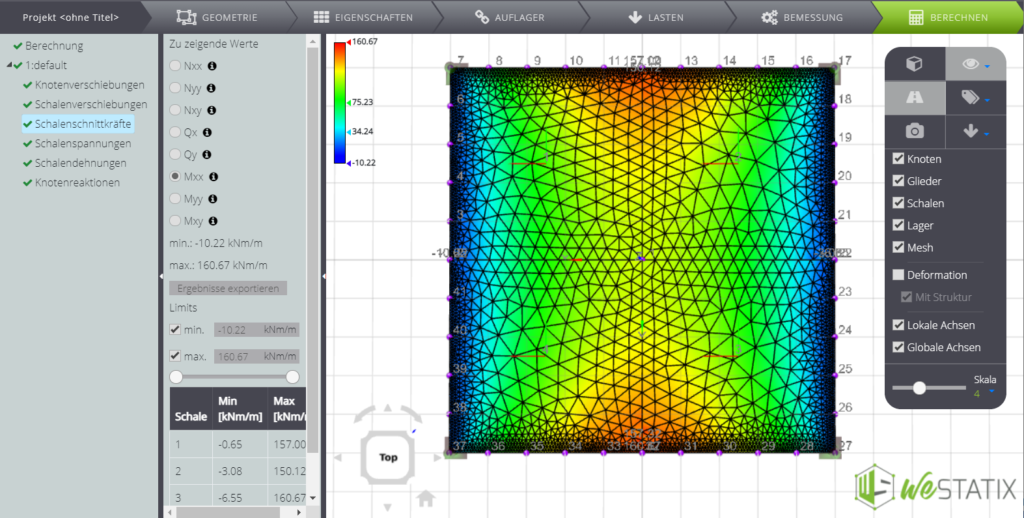
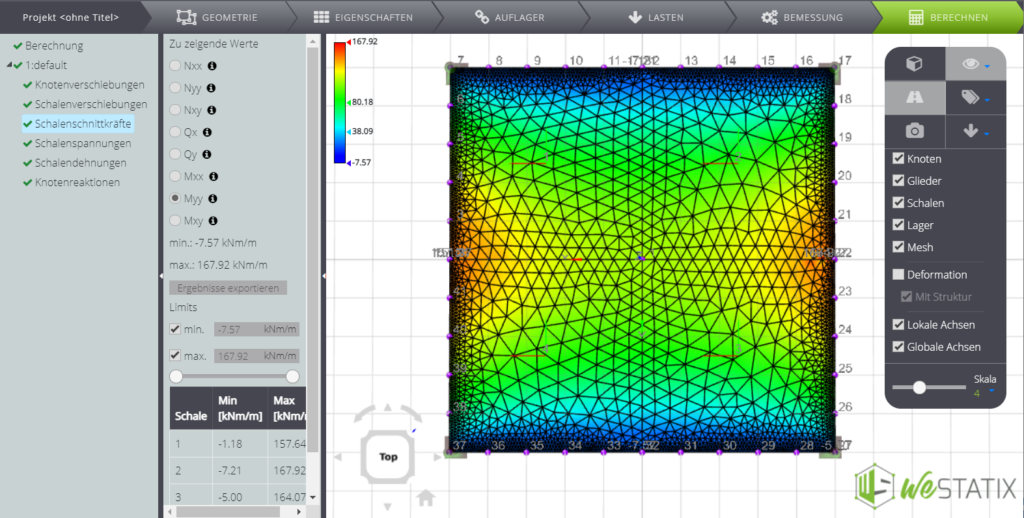
[1] TIMOSHENKO S., WOINOWSKY Y-RIEGER S., Theory of plates and shells, 2ed., McGraw-Hill, New York, 1959.
