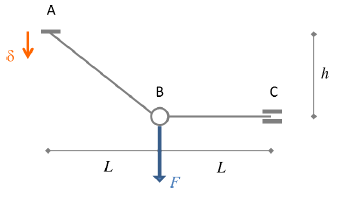
In diesem Querschnitt wollen wir die Genauigkeit von WeStatiX bei der Lösung von dem in der Abbildung unten dargestellte Problem verifizieren. Es besteht aus einer Balkenstruktur mit aufgezwungener Verschiebung eines Auflagers.
Die Daten, die Sie für den Modellaufbau benötigen, sind in der folgenden Tabelle aufgeführt. Sie können auch in unseren Tutorials nachlesen, wie Sie das Modell erstellen können.
| Young’s modulus | E | 200000000 | kPa |
| Querschnittsfläche | A | 0,04 | \(m^2\) |
| Länge | L | 4,00 | m |
| Höhe | h | 3,00 | m |
| Trägheitsmoment | J | 1,00E-04 | \(m^4\) |
| Verschiebung | \(\delta\) | 0,001 | m |
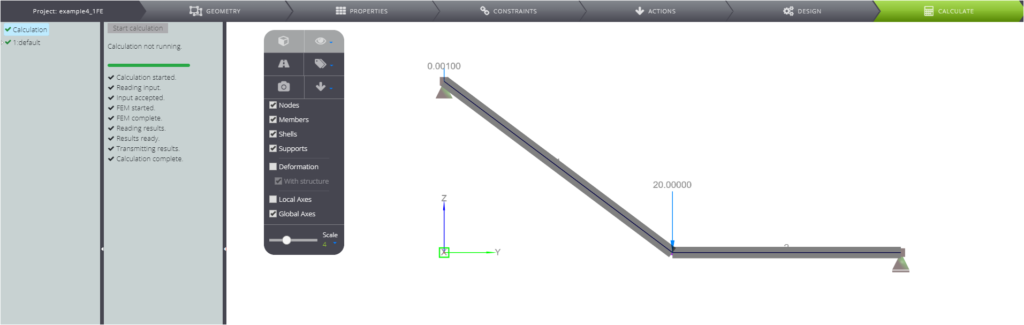
Hier ist das in WeStatiX erstellte Modell, wie Sie es in der graphischen Oberfläche sehen können.
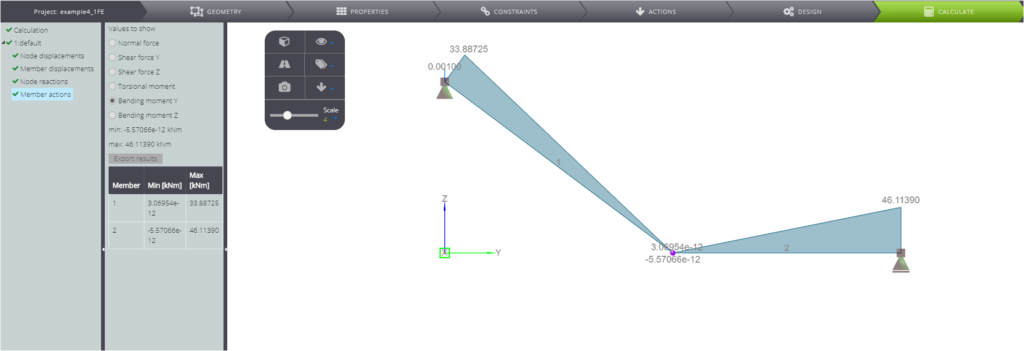
Wie üblich können Sie die Balkengleichung lösen, um die analytische Ergebnisse für alle Durchbiegungen, Drehungen und Schnittgrößen zu finden. In der untenstehenden Tabelle vergleichen wir die grundlegenden Ergebnisse, die wir analytisch erhalten haben, mit den numerischen Ergebnissen, die wir in WeStatiX erhalten haben.
| BESCHREIBUNG | Parameter | EINH. | ANALYTISCHE LÖSUNG | WSX | Fehler | |
|---|---|---|---|---|---|---|
| Horizontale Reaktion in A | \(H_A\) | kN | \(\) | 0,00 | 0,00 | 0,00% |
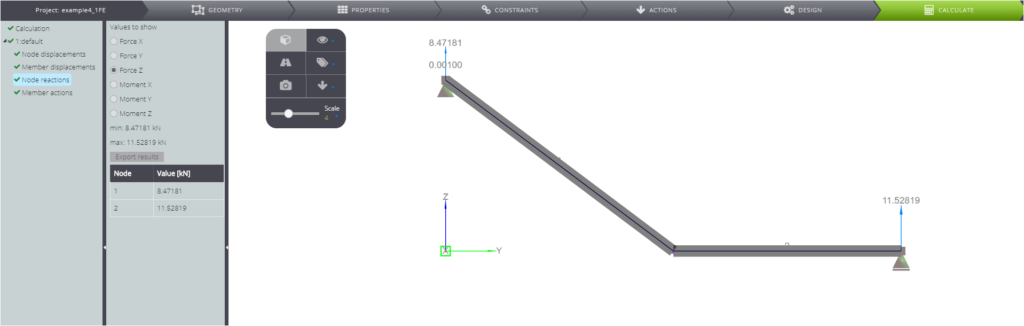
| Vertikale Reaktion in A | \(V_A\) | kN | \(\) | 8,44 | 8,47 | 0,33% |
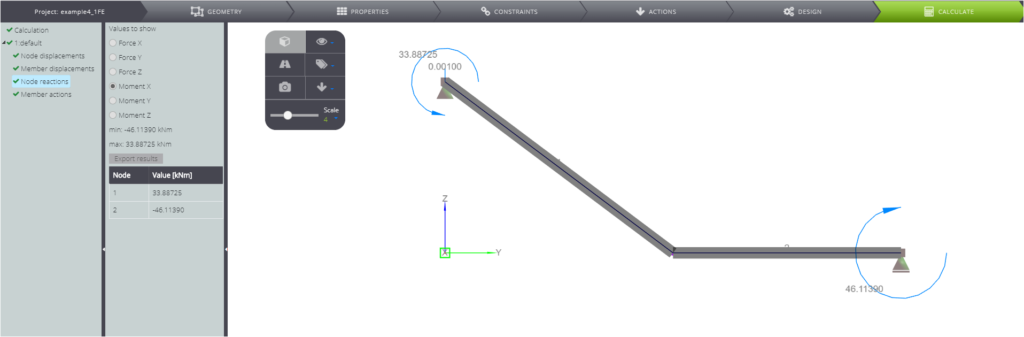
| Moment-Reaktion in A | \(M_A\) | kNm | \(\) | 33,89 | 33,89 | 0,00% |
| Vertikale Reaktion in C | \(V_C\) | kN | \(\) | 11,53 | 11,53 | 0,00% |
| Moment-Reaktion in C | \(M_C\) | kN | \(\) | -46,11 | -46,11 | 0,00% |
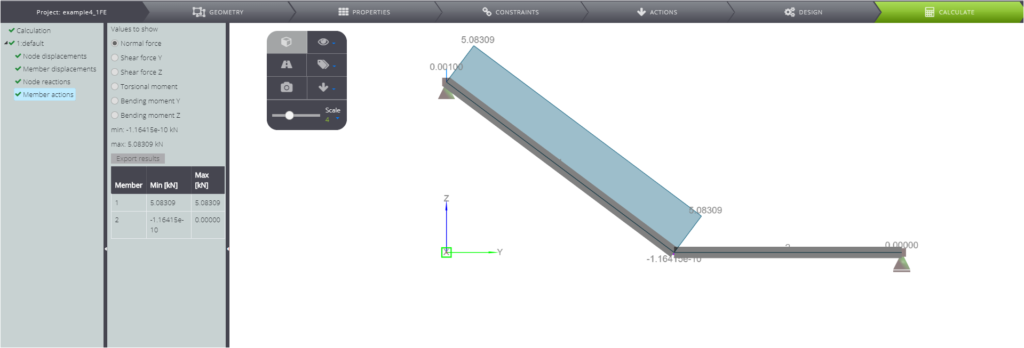
| Normalkraft im Balken 1 | \(N_1\) | kNm | \(\) | 5,08 | 5,08 | 0,06% |
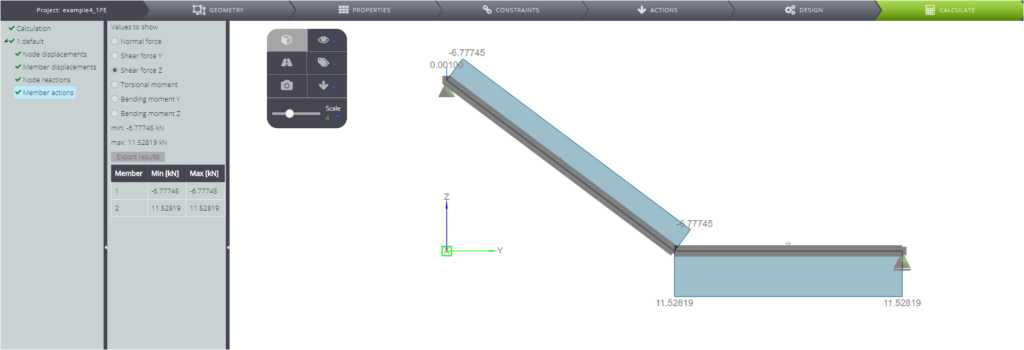
| Querkraft im Balken 1 | \(T_1\) | kN | \(\) | -6,78 | -6,78 | 0,04% |
In den folgenden Bildern können Sie alle numerischen Ergebnisse sehen.