Auf dieser Seite besprechen wir die Ergebnisse des RC-Entwurfs für einen Kragträger, der zweiachsiger Biegung und Längskraft ausgesetzt ist.
| Normalkraft | \(N_{Ed}\) | \(\) | 2000 | kN |
| Biegemoment X | \(M_{Ed,X}\) | \(\) | 234 | kNm |
| Biegemoment Z | \(M_{Ed,Z}\) | \(\) | 100 | kNm |
Sie finden das Modell in WeStatiX bereit für Ihre Calculate.
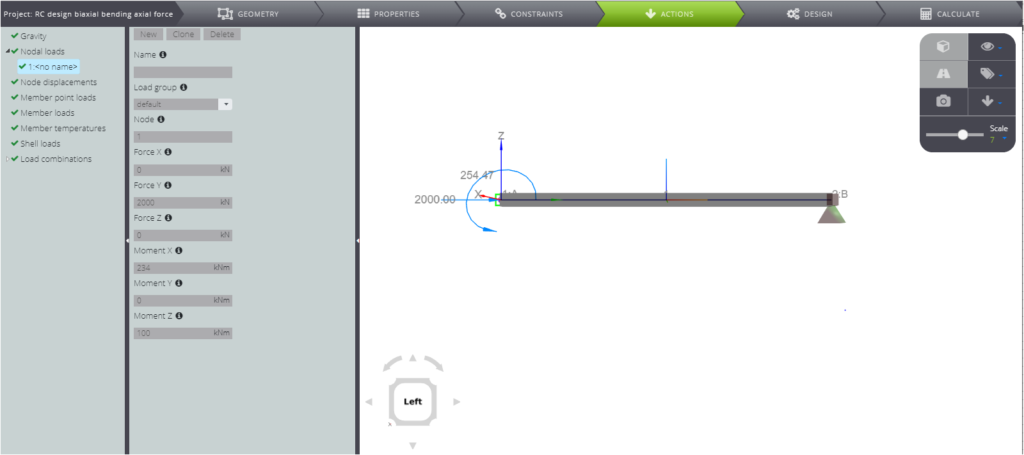
In der folgenden Tabelle können Sie die Querschnittsparameter ablesen
| BESCHREIBUNG | SYMBOL | WERT | UM | |
|---|---|---|---|---|
| Gesamtbreite eines Querschnitts | \(b\) | \(\) | 300 | mm |
| Höhe | \(h\) | \(\) | 400 | mm |
| Obere Betondeckung | \(d_1\) | \(\) | 50 | mm |
| Untere Betondeckung | \(d_2\) | \(\) | 50 | mm |
| \(d’\) | \(h-d_1\) | 350 | mm | |
| – | \(b’\) | \(b-d_2\) | 250 | mm |
| Verhältnis für die Wahl des Interaktionsdiagramms | \(d’/h\) | \(\) | ,13 | – |
Und die Materialparameter
| BESCHREIBUNG | SYMBOL | WERT | UM | |
|---|---|---|---|---|
| Charakteristische Zylinderdruckfestigkeit von Beton nach 28 Tagen | \(f_{ck}\) | \(\) | 42.500,00 | kPa |
| Charakteristische Fließgrenze der Bewehrung | \(f_{yk}\) | \(\) | 549.700,00 | kPa |
| Koeffizient unter Berücksichtigung von Langzeiteffekten | \(\alpha_{cc}\) | \(\) | 1,00 | – |
| Teilsicherheitsfaktor für Beton | \(\gamma_c\) | \(\) | 1,50 | – |
| Teilsicherheitsfaktor für Beton- oder Spannstahl | \(\gamma_s\) | \(\) | 1,15 | – |
| Bemessungswert der Betondruckfestigkeit | \(f_{cd}\) | \(\alpha_{cc} f_{ck}/\gamma_c\) | 28.333,33 | kPa |
| Bemessungswert für die Fließgrenze der Bewehrung | \(f_{yd}\) | \(f_{yk}/\gamma_{s}\) | 478.000,00 | kPa |
Wenn Sie einen Blick auf die Ergebnisse der Bemessung von Stahlbetongliedern werfen, werden Sie feststellen, dass die Gesamtfläche der Bewehrung \(A_{s,tot}\) beträgt \(29,02 cm^2\).
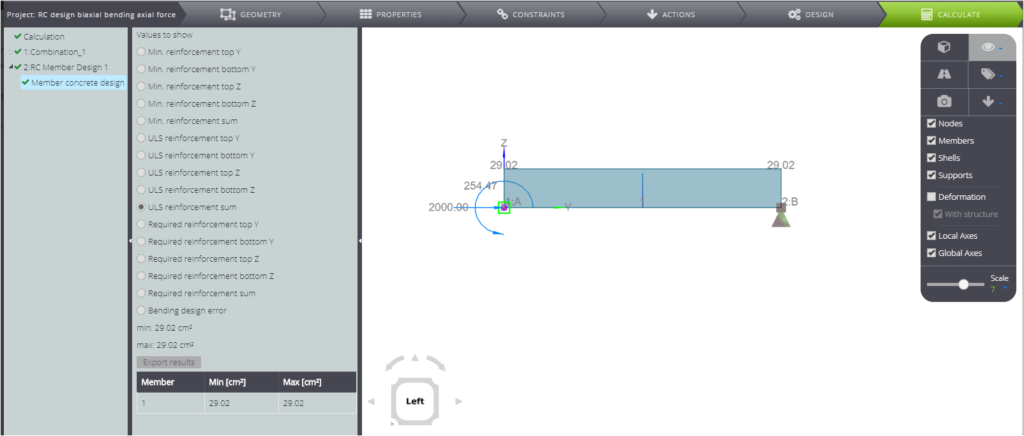
Sie können dies mit Hilfe der Interaktionsdiagramme überprüfen, wie in [1] vorgeschlagen. Demnach müssen Sie die folgenden Parameter finden
| \(\beta\) | \(1-N_d/b \cdot h \cdot f_{ck}\) | 0,61 | – | |
| Wirksames uniaxiales Moment | \(M’_z\) | \(M_x+\beta M_y d/b’ \) | 322,64 | kNm |
| Parametrisierte Normalkraft | \(\nu\) | \(N_d/b \cdot h \cdot f_{cd}\) | 0,59 | – |
| Parametriertes Biegemoment | \(\mu\) | \(M’_z/b\cdot h^2 \cdot f_{cd}\) | 0,24 | – |
Sie müssen also die unten gezeigten Interaktionsdiagramme für die Bemessung für biaxiale Biegung und Längskraft für einen Querschnitt mit d’/h=0,10 and d’/h=0,15, berücksichtigen
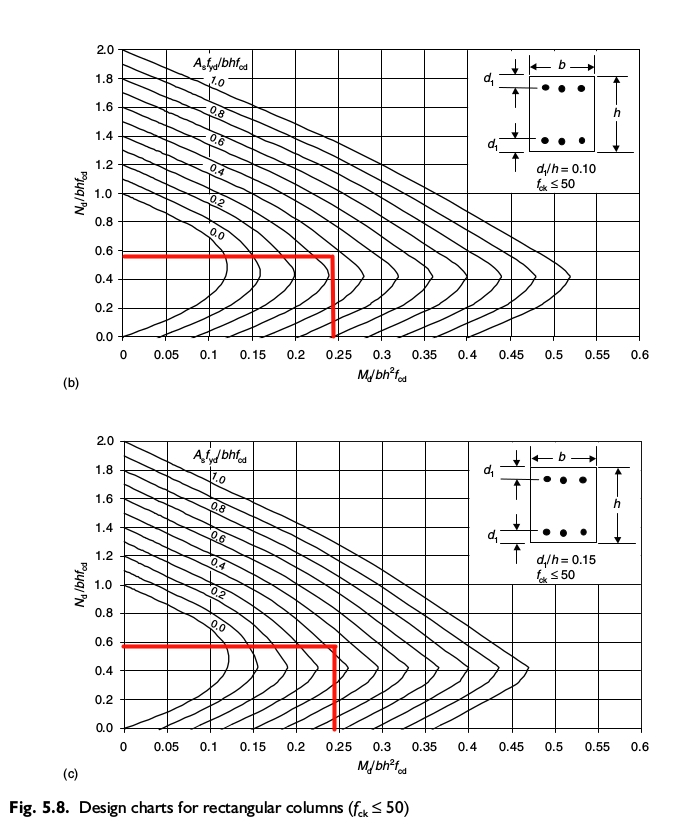
Dann ist es einfach, die Gesamtfläche der Bewehrung zu finden
| Koeffizient aus Interaktionsdiagramm | \(A_s \cdot f_{yd} / b \cdot h \cdot f_{cd}\) | \(\) | 0,41 | – |
| Gesamtbewehrungsfläche | \(A_{s,tot}\) | \(\) | 29,16 | cm^2 |
Schließlich können Sie den Fehler wie folgt berechnen
WeStatiX berechnet korrekterweise die Lösung.
[1] A.W.. BEEBY and R.S: NARAYANAN – Designers’ guide to Eurocode 2: design of concrete structures. – Designers’ guide to EN1992-1-1 and EN1992-1-2 Eurocode 2: design of concrete structures. General rules and rules for buildings and structural fire design.
