Um die Bemessung eines Stahlbetonträgers nachzuweisen, betrachten wir den unten dargestellten rechteckigen Stahlbetonquerschnitt.
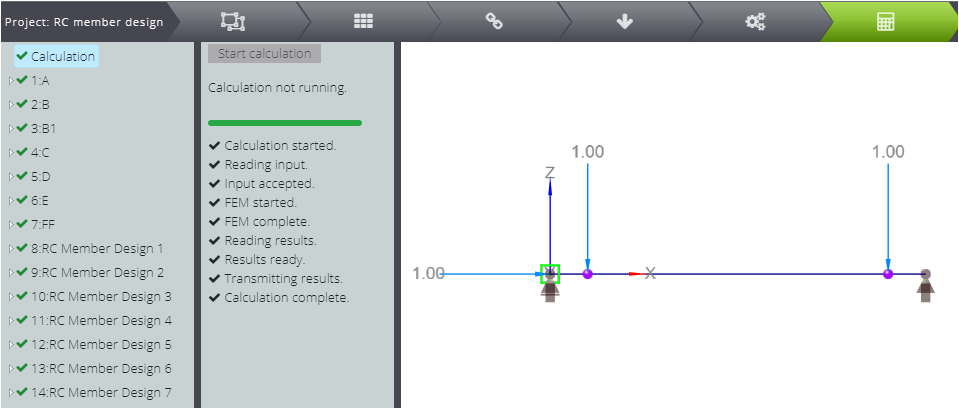
Es handelt sich um einen einfach abgestützten 10 m langen Balken mit zwei Punktlasten, die sich im Abstand von 1 m von den Auflagern befinden.
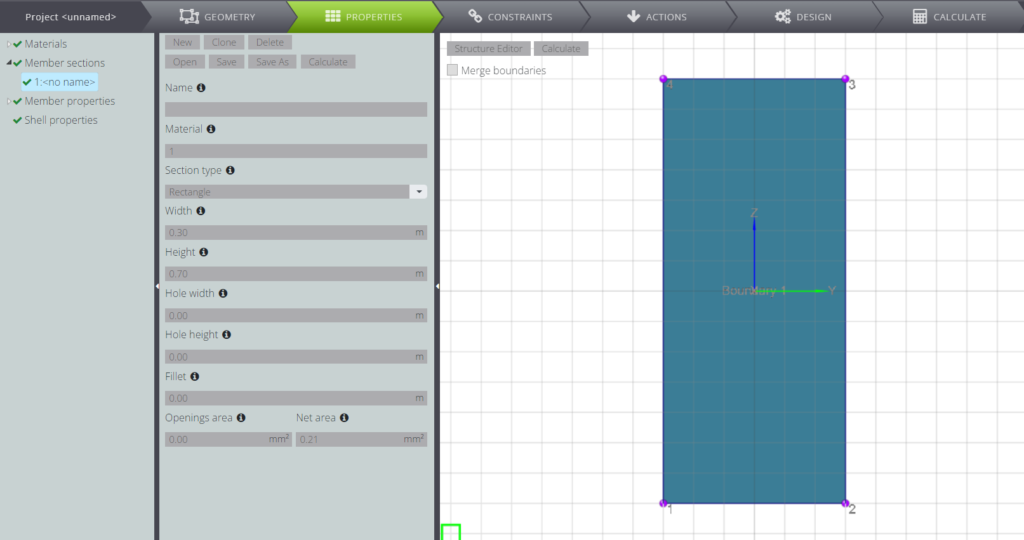
Die Querschnittseigenschaften sind in der folgenden Tabelle dargestellt.
| BESCHREIBUNG | SYMBOL | WERT | UM | |
|---|---|---|---|---|
| Breite | \(b\) | \(\) | 30,0 | cm |
| Höhe | \(h\) | \(\) | 70,0 | cm |
| Untere Betondeckung | \(c\) | \(\) | 50 | mm |
| Obere Betondeckung | \(c’\) | \(\) | 50 | mm |
| Effektive Querschnittstiefe | \(d\) | \(h-c\) | 65,0 | cm |
| \(z_S\) | \(h-c-c’\) | 60,0 | cm | |
| \(z_{s1}\) | \(h/2-c\) | 60,0 | cm | |
| \(z_{s2}\) | \(h/2-c’\) | 60,0 | cm |
Sie können das Modell auch in WeStatiX finden oder dank unseres Tutorials entdecken, wie man es aufbaut.
ERGEBNISSE
Sehen Sie sich nun die Ergebnisse genau an: Sie können sie für jede Lastkombination und für jeden Bemessungsfall von Stahlbetonbauteilen untersuchen. Sie werden die Linearkombination der folgenden Diagramme sein.
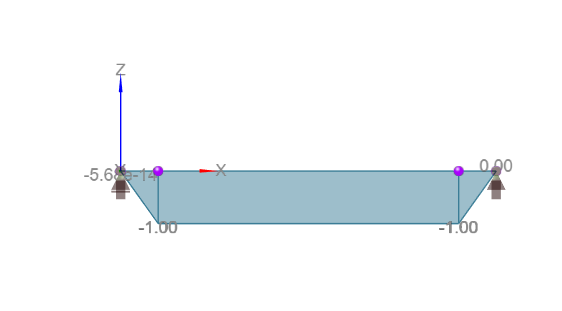
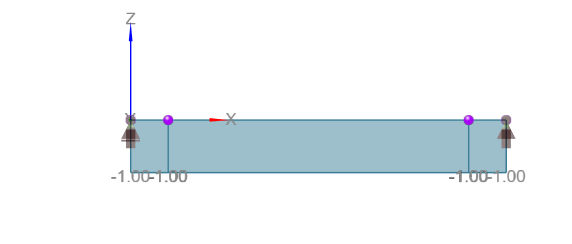
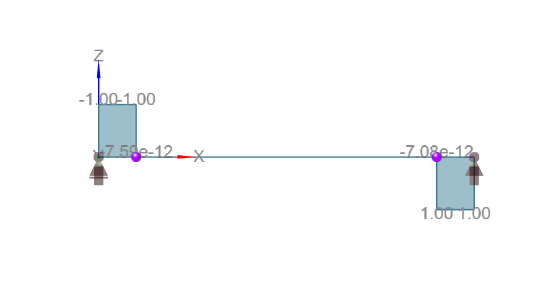
Wie Sie sehen, wird das Member 2 niemals Querkräften ausgesetzt. Die Bemessung des Querschnitts des Stahlbetonträgers wird daher nur für dieses Member für die sechs in der Tabelle aufgeführten Fälle durchgeführt.
| CASE | A | B | C | D | E | F | ||
|---|---|---|---|---|---|---|---|---|
| Biegemoment [kNm] | \(M_{Ed}\) | 500 | 1500 | 1000 | 1000 | 400 | 300 | |
| Axiale Kraft[kN] | \(N_{Ed} \) | 0 | 0 | 1000 | 1800 | 2000 | 2000 |
Hier konzentrieren wir uns auf die Ergebnisse der Bemessung von Stahlbetonbauteilen und vergleichen sie mit denen, die wir nach den Richtlinien der Norm EN-1992-1-1 erhalten können. [1]
Die Materialparameter sind in der nachstehenden Tabelle aufgeführt.
| BESCHREIBUNG | SYMBOL | FORMBLATT | WERT | UM |
|---|---|---|---|---|
| Charakteristische Zylinderdruckfestigkeit von Beton nach 28 Tagen | \(f_{ck}\) | \(\) | 25.000 | kPa |
| Charakteristische Fließgrenze der Bewehrung | \(f_{yk}\) | \(\) | 420.000 | kPa |
| Koeffizient für Berücksichtigung von Langzeiteffekten | \(\alpha_{cc}\) | \(\) | 1,00 | – |
| Teilsicherheitsfaktor für Beton | \(\gamma_c\) | \(\) | 1,50 | – |
| Teilsicherheitsfaktor für Beton- oder Spannstahl | \(\gamma_s\) | \(\) | 1,15 | – |
| Bemessungswert der Betondruckfestigkeit | \(f_{cd}\) | \(\alpha_{cc} f_{ck}/\gamma_c\) | 16.670 | kPa |
| Bemessungswert für die Fließgrenze der Bewehrung | \(f_{yd}\) | \(f_{yk}/\gamma_{s}\) | 365.220 | kPa |
In den Diagrammen können Sie die Spannungs-Dehnungs-Beziehungen für Beton und für Bewehrungsstahl sehen.
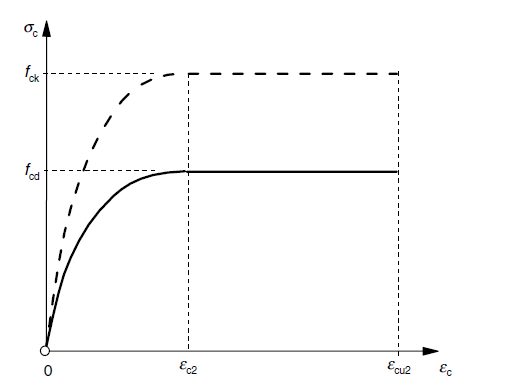
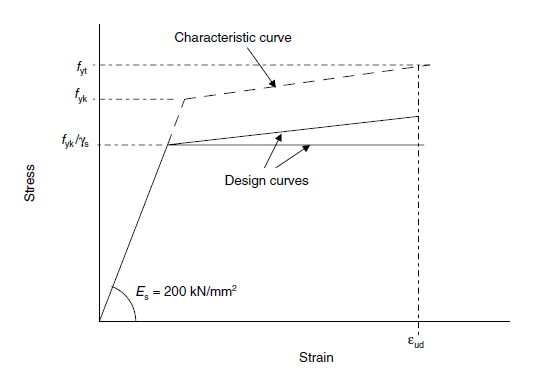
Unter Berücksichtigung der Materialparameter und der Querschnitteigenschaften können Sie die folgenden Parameter berechnen.
| \(x_{lim}\) | \(\frac{700 \cdot d}{f_{yd [MPa]}+700}\) | 42,71 | cm | |
| \(F_{cd,lim}\) | \(0,8095 \cdot x_{lim} \cdot b \cdot f_{cd}\) | 1.728,86 | kN |
Sie helfen Ihnen, verschiedene Spannungszustände auf den Querschnitten zu definieren.
FALL A
Im ersten Fall wird der mittlere Teil des Balkens reinen Biegebedingungen ausgesetzt.
| Biegemoment | \(M_{Ed}\) | \(\) | 500 | kNm |
| Normalkraft | \(N_{Ed}\) | \(\) | 0 | kN |
Für die Berechnung der Bewehrungsfläche ist es notwendig, den folgenden Parameter zu berechnen, wie in [1] beschrieben.
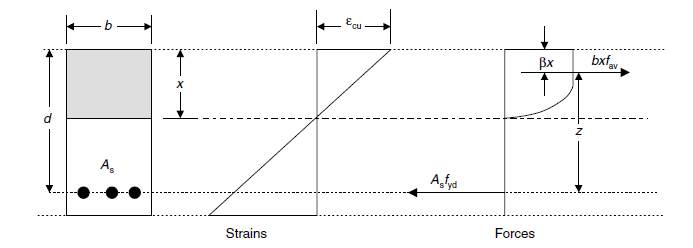
| BESCHREIBUNG | SYMBOL | FORMBLATT | WERT | UM |
|---|---|---|---|---|
| \(M_{S1}\) | \(M_{s1} =M_{Ed}\) | 500 | kNm | |
| Tiefe der neutralen Achse | \(x\) | \(1,202\left(d-\sqrt{d^2-\frac{2,055 \cdot M_{s1}}{b\cdot f_{cd}}}\right)\) | 22,1 | cm |
| \(x<x_{lim}\) | ||||
| \(F_{cd}\) | \(0,8095 \cdot x \cdot b \cdot f_{cd}\) | 895,99 | kN | |
| \(M_{cd1}\) | \(F_{cd}\cdot(d-0,4160x)\) | 499,88 | kNm |
In diesem Fall ist der Träger einfach bewehrt und Sie können die Lösung für den Querschnitt des Bewehrungsstahls leicht berechnen.
| ANALYTICAL | WSX | ERROR | |||
|---|---|---|---|---|---|
| Querschnittsfläche der Bewehrung (unten) [cm^2] | \(A_{s1}’\) | \(\frac{F_{cd}-N}{f_{yd}}\) | 24,53 | 24,54 | 0,04% |
Die Ergebnisse für den Bemessung von Stahlbetonbauteilen sind in der folgenden Abbildung dargestellt.
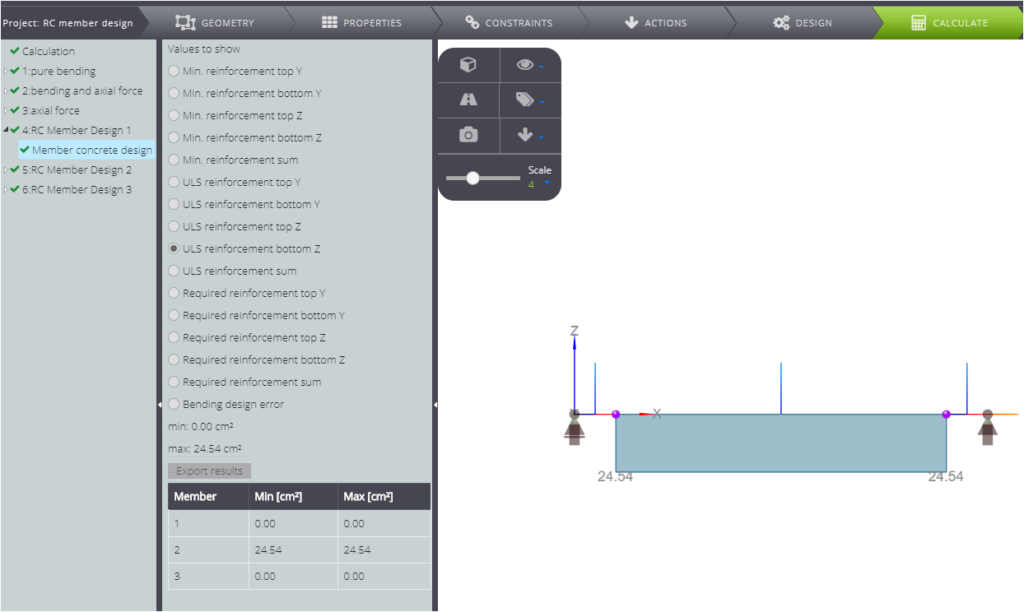
Sie trifft perfekt die Ergebnissen, die wir nach dem Standard erhalten haben.
FALL B
Wie im Fall A ist die Normalkraft null, aber das Biegemoment ist größer.
| Biegemoment | \(M_{Ed}\) | \(\) | 1500 | kNm |
| Normalkraft | \(N_{Ed}\) | \(\) | 0 | kN |
Dies führt Sie zu folgender Berechnung.
| BESCHREIBUNG | SYMBOL | FORMBLATT | WERT | UM |
|---|---|---|---|---|
| \(M_{S1}\) | \(M_{s1} =M_{Ed}\) | 1500 | kNm | |
| Tiefe der neutralen Achse | \(x\) | \(1,202\left(d-\sqrt{d^2-\frac{2,055 \cdot M_{s1}}{b\cdot f_{cd}}}\right)\) | – | cm |
| \(\sqrt{\cdot}<0\) | ||||
| Tiefe der neutralen Achse | \(x\) | \(x=x_{lim}\) | 42,71 | cm |
| \(F_{cd}\) | \(0,8095 \cdot x \cdot b \cdot f_{cd}\) | 1.728,86 | kN |
Angesichts der größeren Einheit des Biegemoments müssen Sie in diesem Fall auch oben auf dem Querschnitt einen Verstärkungsbereich anbringen. Sie können die Querschnittsfläche für die untere und obere Bewehrung berechnen und mit den Ergebnissen von WeStatiX vergleichen.
| ANALYTIKALISCHE | WSX | FEHLER | |||
|---|---|---|---|---|---|
| Querschnittsfläche der Bewehrung (unten) [cm^2] | \(A_{s1}\) | \(\frac{F_{cd}+A_{s2} \cdot f_{yd}-N}{f_{yd}}\) | 78,53 | 78,53 | 0,00% |
| Querschnittsfläche der Bewehrung (oben) [cm^2] | \(A_{s2}\) | \(\frac{M_{s1}-M_{cd1}}{f_{yd}\cdot z_s}\) | 31,19 | 31,19 | 0,00% |
Wie Sie sehen, stimmen die beiden Lösungen überein.
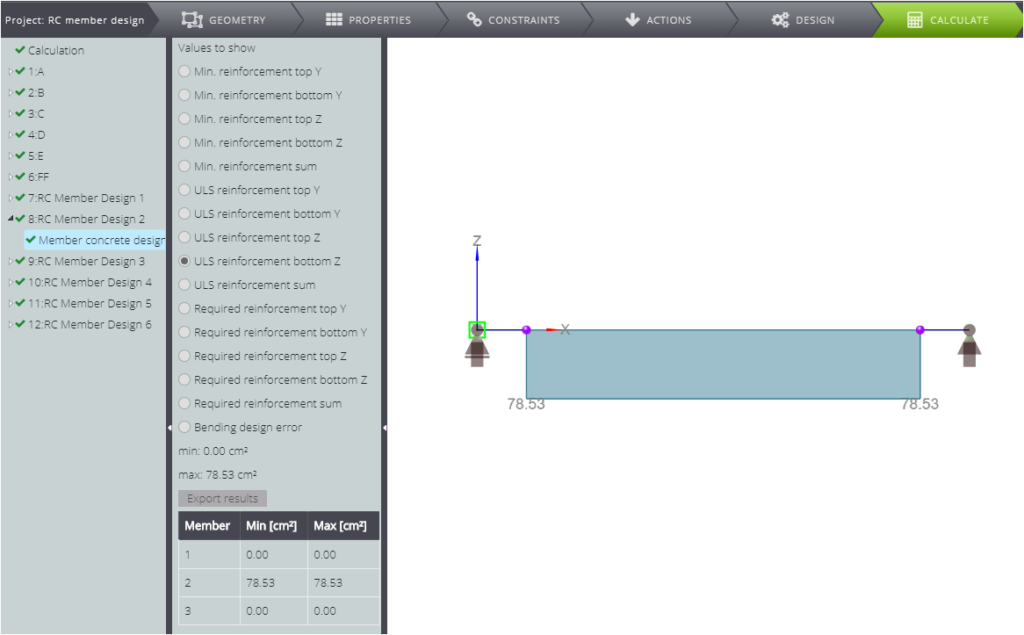
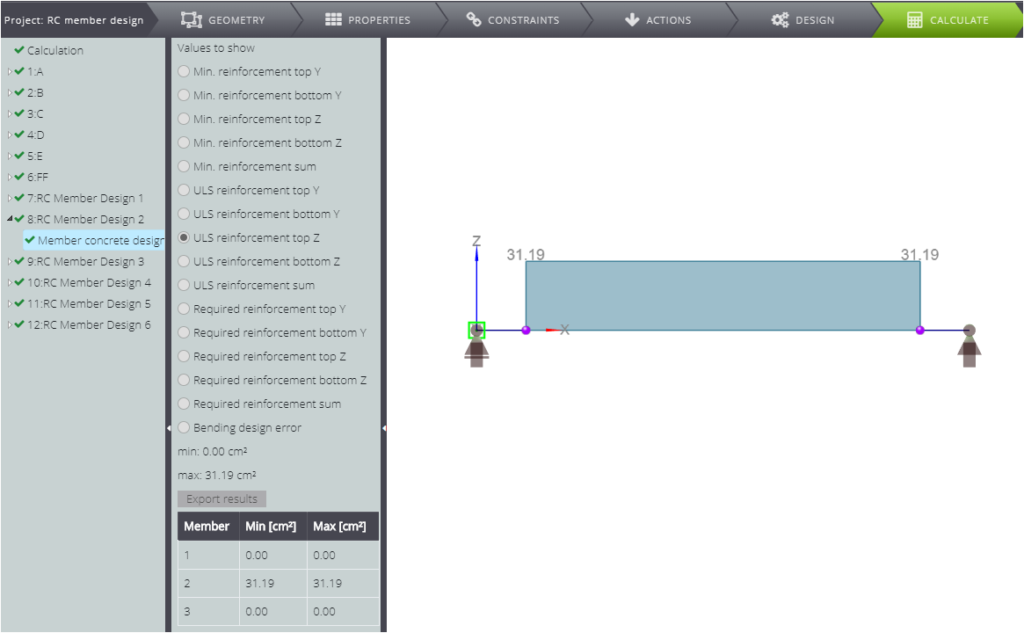
FALL C
In diesem Fall hängt die Querschnittsspannung vom Biegemoment, aber auch von der Normalkraft ab.
| Biegemoment | \(M_{Ed}\) | \(\) | 1000 | kNm |
| Normalkraft | \(N_{Ed}\) | \(\) | 1000 | kN |
Um den Bewehrung zu berechnen, müssen Sie die in der Tabelle angezeigten Parameter berechnen.
| Description | Symbol | Formula | value | UM |
|---|---|---|---|---|
| \(M_{S1}\) | \(M_{s1} =M_{Ed}+N_{Ed}\cdot z_{s1}\) | 1300 | kNm | |
| Tiefe der neutralen Achse | \(x\) | \(1,202\left(d-\sqrt{d^2-\frac{2,055 \cdot M_{s1}}{b\cdot f_{cd}}}\right)\) | – | cm |
| \(\sqrt{\cdot}<0\) | ||||
| Tiefe der neutralen Achse | \(x\) | \(x=x_{lim}\) | 42,71 | cm |
| \(F_{cd}\) | \(0,8095 \cdot x \cdot b \cdot f_{cd}\) | 1.728,86 | kN |
Jetzt können Sie, wie im vorigen Fall, die Bewehrungsflächen berechnen und sie mit den numerischen Ergebnissen vergleichen.
| ANALYTIKALISCHE | WSX | FEHLER | |||
|---|---|---|---|---|---|
| Querschnittsfläche der Bewehrung (unten) [cm^2] | \(A_{s1}\) | \(\frac{F_{cd}+A_{s2} \cdot f_{yd}-N}{f_{yd}}\) | 42,02 | 42,01 | 0,02% |
| Querschnittsfläche der Bewehrung (oben) [cm^2] | \(A_{s2}\) | \(\frac{M_{s1}-M_{cd1}}{f_{yd}\cdot z_s}\) | 22,06 | 22,05 | 0,05% |
Auch in diesem Fall wird die WeStatiX-Lösung für die Bemessung eines Stahlbetonträgers nachgewiesen.
FALL D
Betrachten wir nun den Spannungszustand, wenn man die Normalkraft erhöht.
| Biegemoment | \(M_{Ed}\) | \(\) | 1000 | kNm |
| Normalkraft | \(N_{Ed}\) | \(\) | 1800 | kN |
Im Gegensatz zum vorherigen Fall ist die Druckkraft \(N > F_{cd,lim} \)
Berechnen Sie wiederum die folgenden Parameter.
| BESCHREIBUNG | SYMBOL | FORMBLATT | WERT | UM |
|---|---|---|---|---|
| \(M_{S1}\) | \(M_{Ed}+N_{Ed}\cdot z_{s1}\) | 1540 | kNm | |
| \(M_{S2}\) | \(M_{s2} =M_{Ed}-N_{Ed}\cdot z_{s2}\) | 460 | kNm | |
| Tiefe der neutralen Achse | \(x\) | \(1,202\left(c’-\sqrt{c’^2-\frac{2,055 \cdot M_{s1}}{b\cdot f_{cd}}}\right)\) | – | cm |
| \(\sqrt{\cdot}<0\) | ||||
| Tiefe der neutralen Achse | \(x\) | \(x=x_{lim}\) | 42,71 | cm |
| \(F_{cd}\) | \(0,8095 \cdot x \cdot b \cdot f_{cd}\) | 1.728,86 | kN |
Und schließlich berechnen Sie die Querschnittsflächen für die Bewehrung.
| ANALYTIKALISCHE | WSX | FEHLER | |||
|---|---|---|---|---|---|
| Querschnittsfläche der Bewehrung (unten) [cm^2] | \(A_{s1}\) | \(\frac{F_{cd}+A_{s2} \cdot f_{yd}-N}{f_{yd}}\) | 31,06 | 31,07 | 0,03% |
| Querschnittsfläche der Bewehrung (oben) [cm^2] | \(A_{s2}\) | \(\frac{M{s1}-M_{cd1}}{f_{yd}\cdot z_s}\) | 33,01 | 33,01 | 0,00% |
Beim Vergleich mit der WeStatiX-Ausgabe des Moduls für die Bemessung von Stahlbetonbalken werden Sie feststellen, dass die Werte gleich sind.
FALL E
Verringern Sie nun das Biegemoment.
| Biegemoment | \(M_{Ed}\) | \(\) | 400 | kNm |
| Normalkraft | \(N_{Ed}\) | \(\) | 2000 | kN |
Um den Belastungszustand zu definieren, definieren Sie die in der Tabelle aufgeführten Parameter.
| BESCHREIBUNG | Symbol | FORMBLATT | WERT | UM |
|---|---|---|---|---|
| \(M_{S1}\) | \(M_{Ed}+N_{Ed}\cdot z_{s1}\) | 1000 | kNm | |
| \(M_{S2}\) | \(M_{s2} =M_{Ed}-N_{Ed}\cdot z_{s2}\) | -200 | kNm | |
| Tiefe der neutralen Achse | \(x\) | \(1,202\left(c’-\sqrt{c’^2-\frac{2,055 \cdot M_{s1}}{b\cdot f_{cd}}}\right)\) | 41,0 | cm |
| \(x<x_{lim}\) | ||||
| Tiefe der neutralen Achse | \(x\) | \(x=x_{lim}\) | 42,7 | cm |
| \(F_{cd}\) | \(0,8095 \cdot x \cdot b \cdot f_{cd}\) | 1.728,86 | kN |
Sie benötigen nach wie vor Bewehrungsflächen sowohl am oberen als auch am unteren Ende des Querschnitts. Berechnen Sie diese wie folgt.
| \(\) | \(\) | ANALYTIKALISCHE | WSX | FEHLER | |
|---|---|---|---|---|---|
| Querschnittsfläche der Bewehrung (unten) [cm^2] | \(A_{s1}\) | \(\frac{F_{cd}+A_{s2} \cdot f_{yd}-N}{f_{yd}}\) | 0,95 | 0,95 | 0,00% |
| Charakteristische Zylinderdruckfestigkeit von Beton nach 28 Tagen | \(A_{s2}\) | \(\frac{M{s1}-M_{cd1}}{f_{yd}\cdot z_s}\) | 8,37 | 8,37 | 0,00% |
Auch in diesem Fall stimmen die beiden Lösungen überein.
FALL F
Wie Sie in der folgenden Tabelle lesen können, ist das Biegemoment im Vergleich zu FALL D bei gleicher Normalkraft kleiner.
| Biegemoment | \(M_{Ed}\) | \(\) | 300 | kNm |
| Normalkraft | \(N_{Ed}\) | \(\) | 2000 | kN |
Wenn Sie den folgenden Parameter berechnen, können Sie feststellen, dass im Gegensatz zu den vorhergehenden Fällen die Tiefe der neutralen Achse größer ist als \(x_{lim}\)
| BESCHREIBUNG | Symbol | FORMBLATT | WERT | UM |
|---|---|---|---|---|
| \(M_{S1}\) | \(M_{Ed}+N_{Ed}\cdot z_{s1}\) | 900 | kNm | |
| \(M_{S2}\) | \(M_{s2} =M_{Ed}-N_{Ed}\cdot z_{s2}\) | -300 | kNm | |
| Tiefe der neutralen Achse | \(x\) | \(1,202\left(c’-\sqrt{c’^2-\frac{2,055 \cdot M_{s1}}{b\cdot f_{cd}}}\right)\) | 48,6 | cm |
| \(x>x_{lim}; x<h\) | ||||
| \(F_{cd}\) | \(0,8095 \cdot x \cdot b \cdot f_{cd}\) | 1.968,82 | kN |
Dies bedeutet, dass nur der obere Bewehrungsbereich benötigt wird.
| ANALYTIKALISCHE | WSX | FEHLER | |||
|---|---|---|---|---|---|
| Querschnittsfläche der Bewehrung (oben) [cm^2] | \(A_{s2}’\) | \(\frac{N-F_{cd}}{f_{yd}}\) | 0,85 | 0,85 | 0,00% |
Auch hier stimmen die Ergebnisse von WeStatiX mit den analytischen Ergebnissen überein.
[1] Skriptum zur Vorlesung BETONBAU 1 nach EC 1992-1-1, Technische Universität Wien, Institut für Tragkonstruktionen – Herausgegeben von Prof. Dr.-Ing. Johann KOLLEGER
