Auf dieser Seite testen wir die Genauigkeit von WeStatiX bei der Lösung einer Struktur, die aus zwei Kragträgern besteht, die durch ein Fachwerk verbunden sind. Die Daten über Geometrie und Materialeigenschaften sind in der folgenden Tabelle aufgeführt.
| Young’s modulus | E | 1,00 | kPa |
| Länge | H | 0,50 | m |
| Länge | L | 1,00 | m |
| Trägheitsmoment | J | 1,00E00 | \(m^4\) |
| Verteilte Last | q | -1,00 | \(kN/m\) |
| Verdichtete Last | P | -1,00 | \(kN\) |
Sie können das Modell einfach in WeStatiX erstellen, wie wir es in unserem Tutorial zeigen, oder Sie finden es bereits in unseren öffentlichen Projekten.
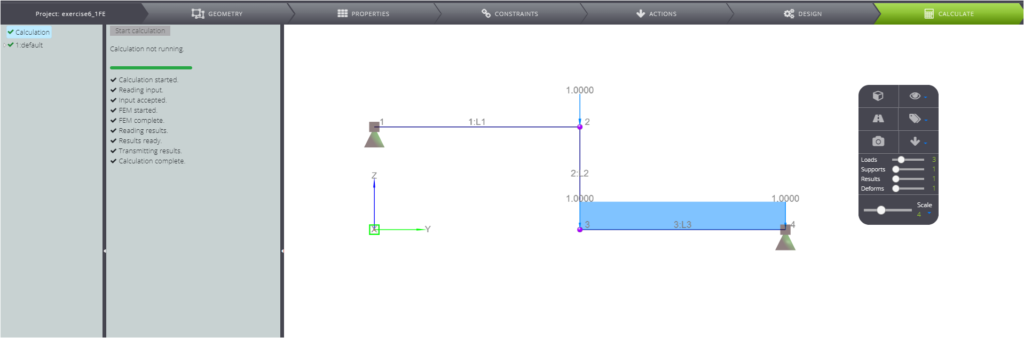
Sie können natürlich die Balkengleichung lösen, um die Analyseergebnisse zu erhalten.
In der folgenden Tabelle werden die Hauptpunkte der Lösung dargestellt und mit den Ergebnissen von WeStatiX verglichen.
| BESCHREIBUNG | Parameter | EINH. | ANALYTISCHE LÖSUNG | ANALYTISCHE LÖSUNG | WSX | FEHLER |
|---|---|---|---|---|---|---|
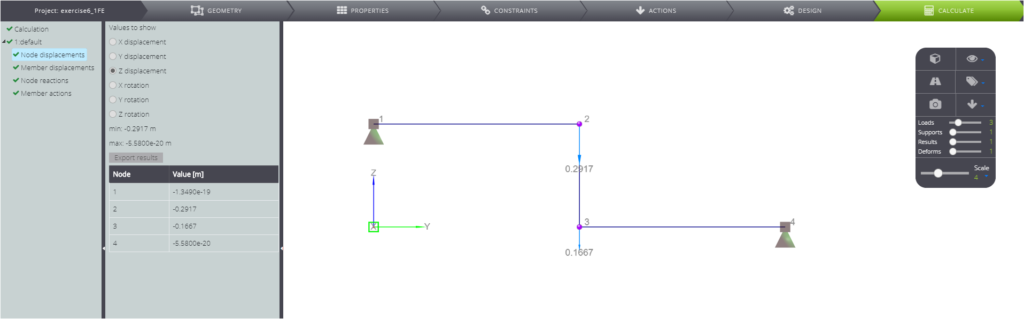
| Vertikale Verschiebung in B | \(v_{B}\) | m | \(7qL^4/24EJ\) | -0,29167 | -0,29170 | 0,01% |
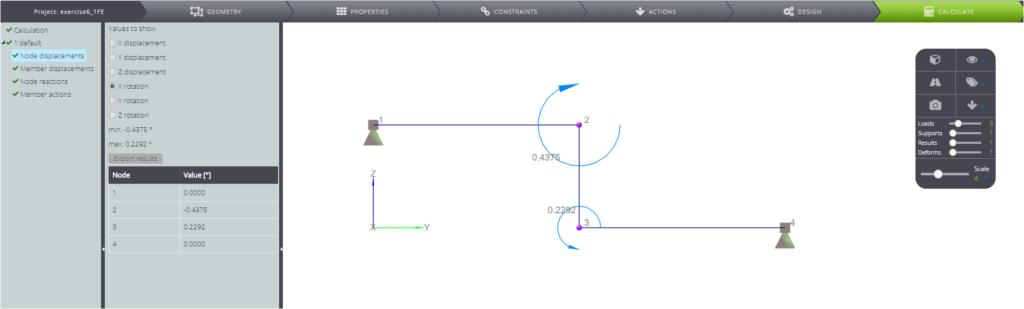
| Drehung in B | \(\phi_B\) | rad | \(7qL^3/16EJ\) | -0,43750 | -0,43750 | 0,00% |
| Vertikale Verschiebung in C (rechts) | \(v_C\) | m | \(1qL^4/6EJ\) | -0,16667 | -0,16670 | 0,02% |
| Drehung in C | \(\phi_C\) | rad | \(11qL^3/48EJ\) | 0,22917 | 0,22920 | 0,01% |
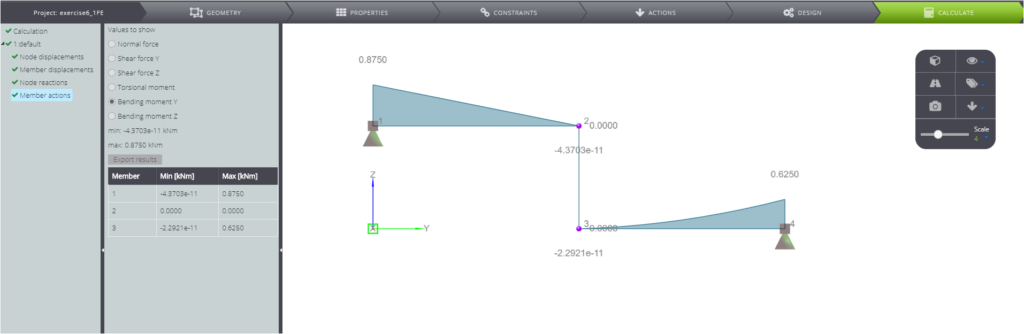
| Biegemoment in A | \(M_A\) | kNm | \(7qL^2/8\) | 0,87500 | 0,87500 | 0,00% |
| Biegemoment in D | \(M_D\) | kNm | \(5qL^2/8\) | 0,62500 | 0,62500 | 0,00% |
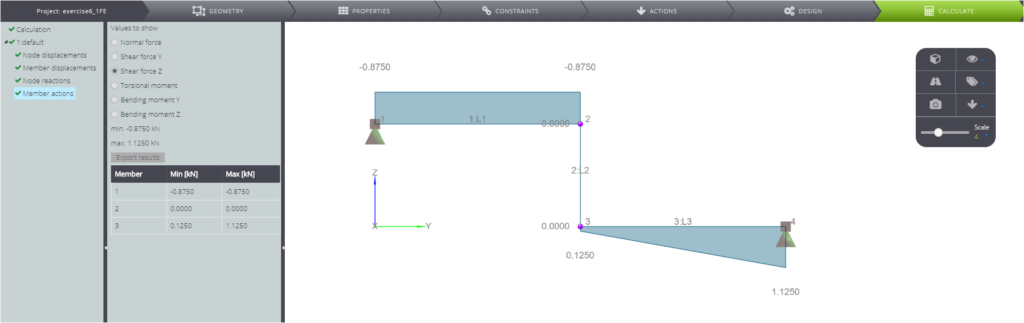
| Querkraft in A | \(T_A\) | kN | \(7qL/8\) | -0,87500 | -0,87500 | 0,00% |
| Querkraft in B (rechts) | \(T_B^{r}\) | kN | \(1qL/8\) | 0,12500 | 0,12500 | 0,00% |
| Querkraft in C | \(T_C\) | kN | \(9qL/8\) | 1,12500 | 1,12500 | 0,00% |
| Normalkraft in B | \(T_B^{r}\) | kN | \(1qL/8\) | -0,12500 | -0,12500 | 0,00% |
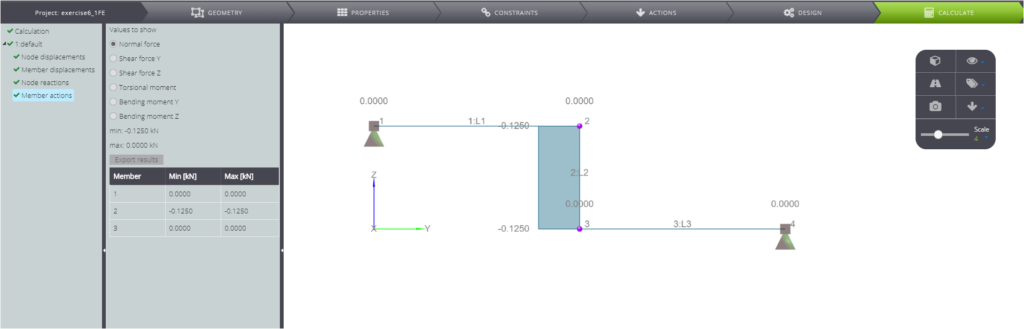
In den folgenden Bildern sehen Sie schließlich die berechneten Ergebnisse.