Betrachten Sie eine gleichmäßig belastete und einfach abgestützte quadratische Platte: Die Daten des Problems sind in der nachstehenden Tabelle aufgeführt.
| Young’s modulus | E | 100.000.000 | kPa |
| Dicke | h | 0,30 | m |
| Poissonzahl | \(\nu\) | 0,30 | – |
| Länge | a | 10,00 | m |
| Gleichmäßiger Druck | q | -10,00 | kPa |
| Biegesteifigkeit der Platte | D | 247252,75 | kN/m |
Die Biegesteifigkeit wird berechnet als \( {E \cdot h^3}/{12(1-\nu^2)}\)
Sie können das Modell in unseren Tutorials in WeStatiX finden. Alternativ können Sie es auch selbst bauen: Wie das geht, können Sie in unserer Dokumentation nachlesen.
Sobald Geometrie, Eigenschaften und Randbedingungen definiert sind, müssen Sie nur noch die Analyse starten, um die Ergebnisse zu erhalten.
Dies ist das Verschiebungsfeld.
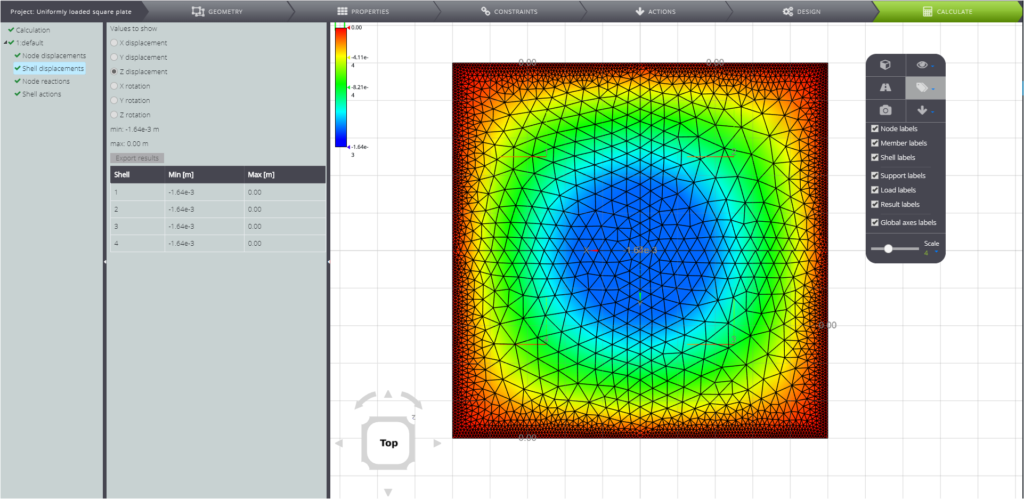
Zweitens, das Biegemoment
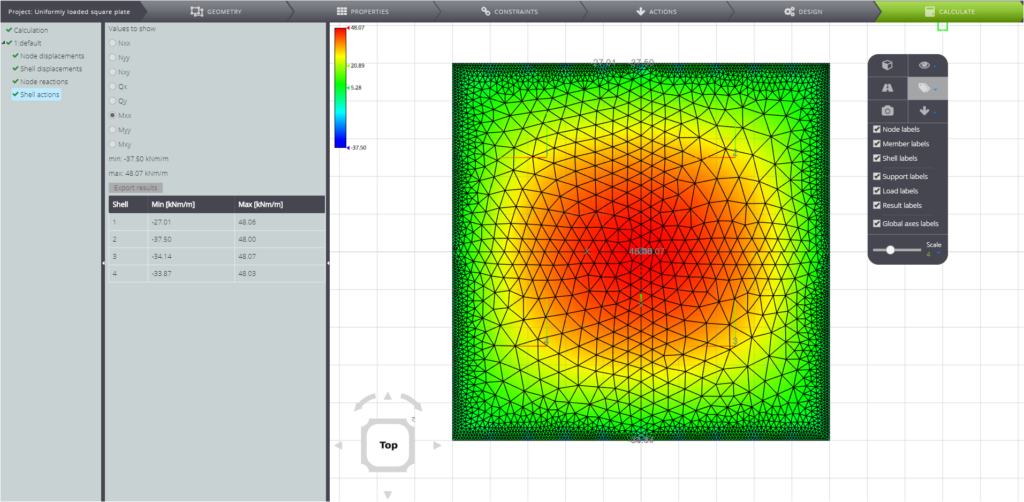
Und schließlich die Knotenkräfte.
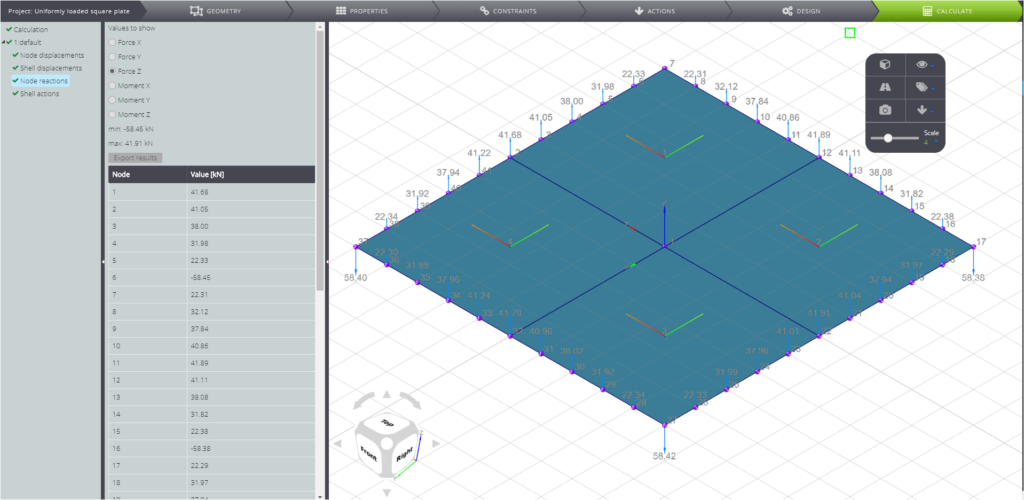
Bitte beachten Sie, dass die Ecken der Platte dazu neigen, unter den Einwirkungen der aufgebrachten Last nach oben zu steigen. Die konzentrierten Kräfte R sind vorhanden, um dies zu verhindern, und sie sind daher nach unten gerichtet. Um den genauen Wert dieser Kräfte zu erfassen, müssen Sie ein feineres Netz herstellen.
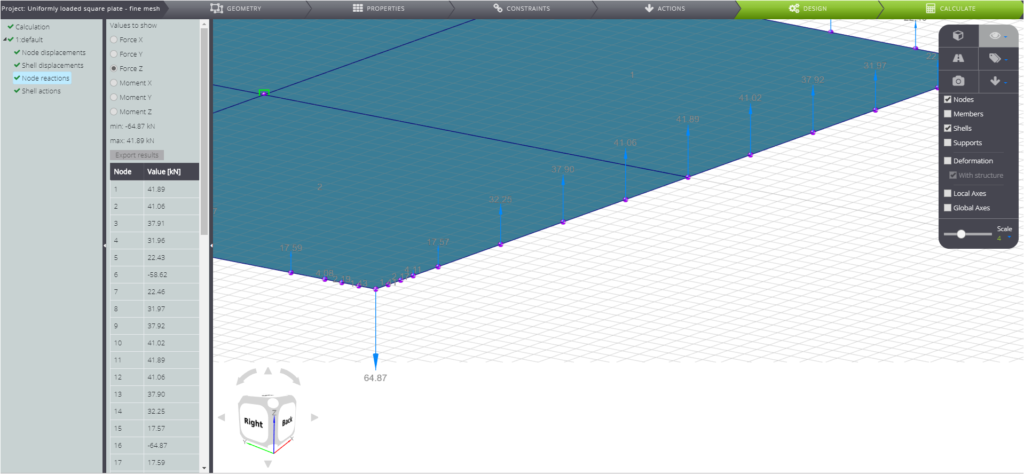
Die analytische Lösung des Problems ist bekannt, und Sie finden sie in Theory of plates and shells [1] .
Im Folgenden vergleichen wir die grundlegenden Punkte der Lösung mit den Ergebnissen, die wir mit unserer FE-Analyse erhalten haben.
| BESCHREIBUNG | Parameter | EINH. | ANALYTISCHE LÖSUNG | WSX – rough mesh | Error- rough mesh |
|---|---|---|---|---|---|
| Durchbiegung | \(w_{max}\) | m | -0.016E-04 | -1,643E-03 | 0,04% |
| Biegemoment | \(M_{x_{max}}\) | kNm/m | -47,90 | -48.07 | 0,35% |
| Reaktionskräfte an den Ecken | R | kN | 65,00 | 58,45 | 11,21% |
Und schließlich der Vergleich mit den Ergebnissen, die mit dem feinsten Netz erzielt wurden.
| BESCHREIBUNG | Parameter | EINH. | ANALYTISCHE LÖSUNG | WSX – fine mesh | FEHLER – fine mesh |
|---|---|---|---|---|---|
| Ablenkung | \(w_{max}\) | m | -0.016E-04 | -0.016E-04 | 0,04% |
| Biegemoment | \(M_{x_{max}}\) | kNm/m | -47,90 | -47,91 | 0,02% |
| Reaktionskräfte an den Ecken | R | kN | 65,00 | 64,87 | 0,20% |
[1] TIMOSHENKO S., WOINOWSKY Y-RIEGER S., Theory of plates and shells, 2ed., McGraw-Hill, New York, 1959.
