In diesem Beispiel wird ein Kragbalken einer konstanten Belastung ausgesetzt: Die Ergebnisse werden vollständig online bestimmt und mit der bekannten analytischen Lösung verglichen.
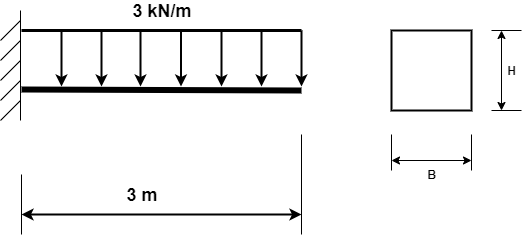
\(E = 210 GPa\)
\(B = H = 0.1 m\)
Definieren Sie das Modell anhand der in der obigen Abbildung gezeigten Daten! In unserem Tutorial beschreiben wir die Vorgangsweise an einem ähnlichen Modell, ansonsten finden Sie es fertig für die Berechnung in WeStatiX, so dass Sie direkt zum Tab CALCULATE gehen und die Analyse ausführen können.
Wir sind bereit, die numerische Lösung mit der analytischen zu vergleichen.
Die analytische Lösung für die Durchbiegung lautet:
\(v(x)= \frac{q_0}{24EI}x^2 (x^2-4Lx +6L^2)\)
Sie können sie leicht erhalten, indem Sie die statische Balkengleichung mit geeigneten Randbedingungen berechnen.
So, jetzt können Sie bekommen:
- die Durchbiegung an der Spitze als \(f = v(L) \frac{q l^4}{8EJ}\)
- die Rotation an der Spitze als \(\phi = \frac{q l^3}{6EJ} \)
- die vertikalen Reaktionskräfte \(V = ql \)
- das Reaktionsmoment kann als \(M = \frac{ql^2}{2} \)
Ergebnis-Vergleich
| ERGEBNISTYP | ZIELWERT | WESTATIX-ERGEBNIS | RELATIVER FEHLER |
|---|---|---|---|
| Durchbiegung am freien Ende [m] | 0.017357 | 0.017357 | 0,00% |
| Rotation am freien Ende [rad] | 0.007714 | 0.007714 | 0,00% |
| Vertikale Reaktionskraft [kN] | 9 | 9 | 0,00% |
| Reaktionsmoment[kNm] | 13.5 | 13.5 | 0,00% |
WeStatiX erfasst vollständig die analytische Lösung.
