Il calcolo strutturale di edifici e infrastrutture viene spesso effettuato utilizzando modelli che rappresentano in modo semplificato i vincoli alla base della struttura. Addirittura, in molti casi, la struttura è vincolata alla base con un vincolo rigido.
Tuttavia, questo approccio non consente di analizzare l’effettivo stato di sollecitazione delle fondazioni e in alcuni casi può anche portare a una valutazione errata della risposta strutturale delle strutture fuori terra. Utilizzo di vincolo a molla può essere un modo efficace per superare questi problemi e ottenere una migliore previsione del comportamento strutturale.
Principali vantaggi dell'utilizzo dei vincoli elastici nella modellazione strutturale
La modellazione dei sostegni di fondazione con vincoli a molla presenta diversi vantaggi. Tra questi, si possono evidenziare tre vantaggi principali:
DESCRIZIONE DEI VINCOLI REALISTICI
È possibile scegliere la costante della molla in base al tipo di terreno di fondazione. Inoltre, è possibile assegnare molle con rigidità diverse in diverse porzioni della zona limite. Infine, è possibile definire vincoli di rotazione a molla, utili, ad esempio, per modellare la rotazione di uno zoccolo alla base di una colonna.
MIGLIORAMENTO DELL’ACCURATEZZA DEL MODELLO
L’uso di vincoli a molla consente di valutare la dimensione corretta dei picchi di deformazione e la loro posizione. Inoltre, permette di calcolare correttamente le forze che agiscono sulle strutture di fondazione e di conseguenza di dimensionarle correttamente. Non meno importante, è possibile considerare l’interazione suolo-struttura e ottenere una risposta realistica delle strutture fuori terra.
MAGGIORE AFFIDABILITÀ DEL PROGETTO
È possibile analizzare la risposta strutturale valutando diversi valori di rigidezza per il terreno e le membrature di fondazione, ottenendo inviluppi di forze agenti. In questo modo è possibile tenere conto delle possibili incertezze del modello, dovute all’incertezza nella conoscenza del tipo di suolo e della sua variabilità.
Modellare le fondazioni come travi di Winkler
Il modello di Winkler si basa sull’ipotesi che il terreno, in un generico punto, si deformi proporzionalmente alla forza normale che agisce su di esso. La deformazione è indipendente da quella degli altri punti e dipende linearmente dalla forza applicata.
La costante di proporzionalità 
Il modello di Winkler è particolarmente utile per modellare il comportamento delle travi di fondazione elastiche, spesso impiegate come strutture di fondazione nei casi in cui non è suggerito il plinto di fondazione. Se le travi di fondazione vengono calcolate considerando i pilastri come vincoli rigidi e la pressione del terreno come un carico distribuito, i momenti flettenti e le forze di taglio ottenuti portano tipicamente a un sovradimensionamento delle travi di fondazione.
Impiegando vincoli elastici a molla basati sulla costante del terreno di Winkler, è possibile ottenere risultati più accurati. Nella figura seguente è rappresentata schematicamente una fondazione a trave Winkler. La rigidità della molla è data dalla costante del terreno moltiplicata per la larghezza della trave.
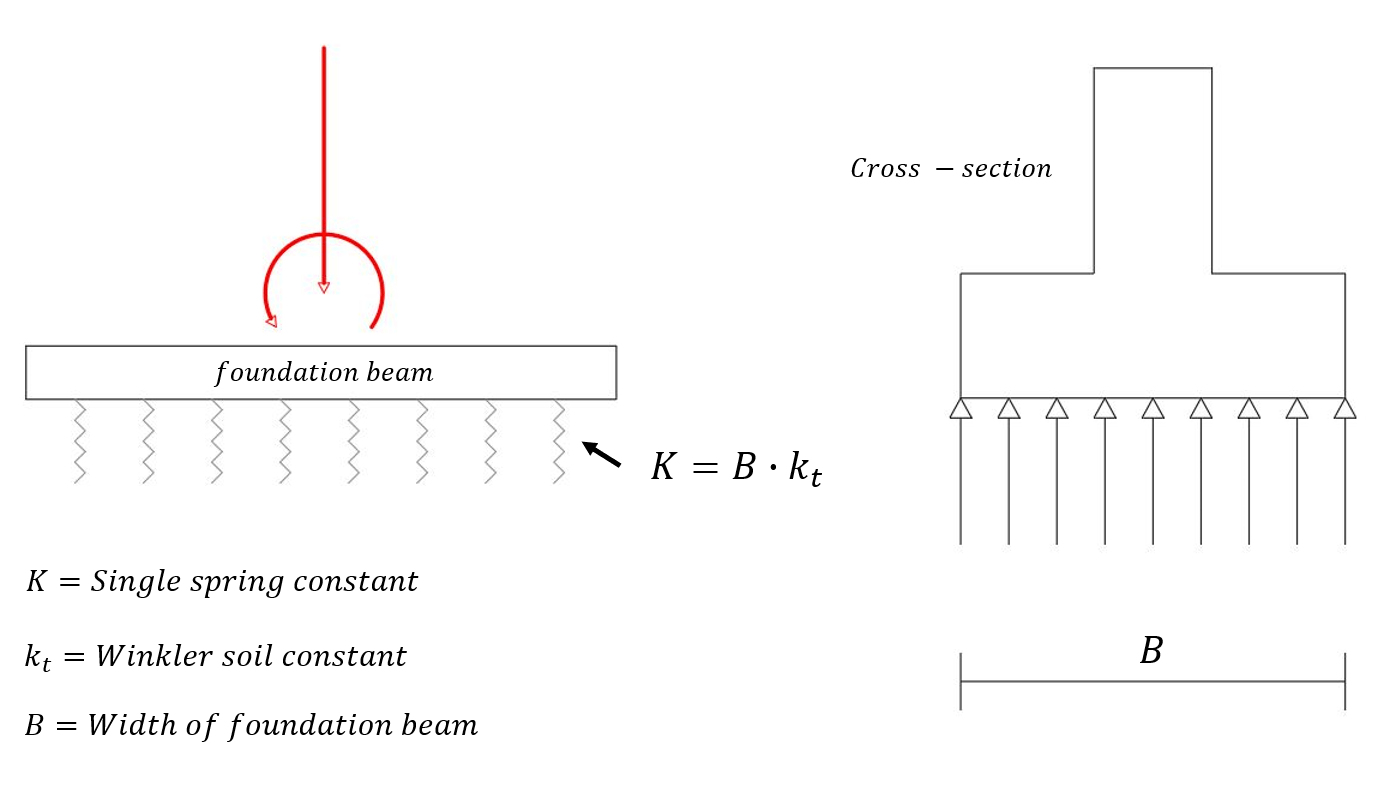
Calcolo di una trave di fondazione con il supporto del terreno di Winkler
Qui mostriamo un esempio di calcolo di una trave di fondazione utilizzando i supporti del terreno di Winkler. Il sistema studiato è mostrato nella figura seguente. La trave è soggetta a un’azione distribuita dovuta ai carichi morti. Inoltre, le colonne esercitano azioni di taglio e momenti flettenti concentrati in alcune sezioni della trave. L’esempio è tratto dal lavoro di
Colajanni et al.
[1].
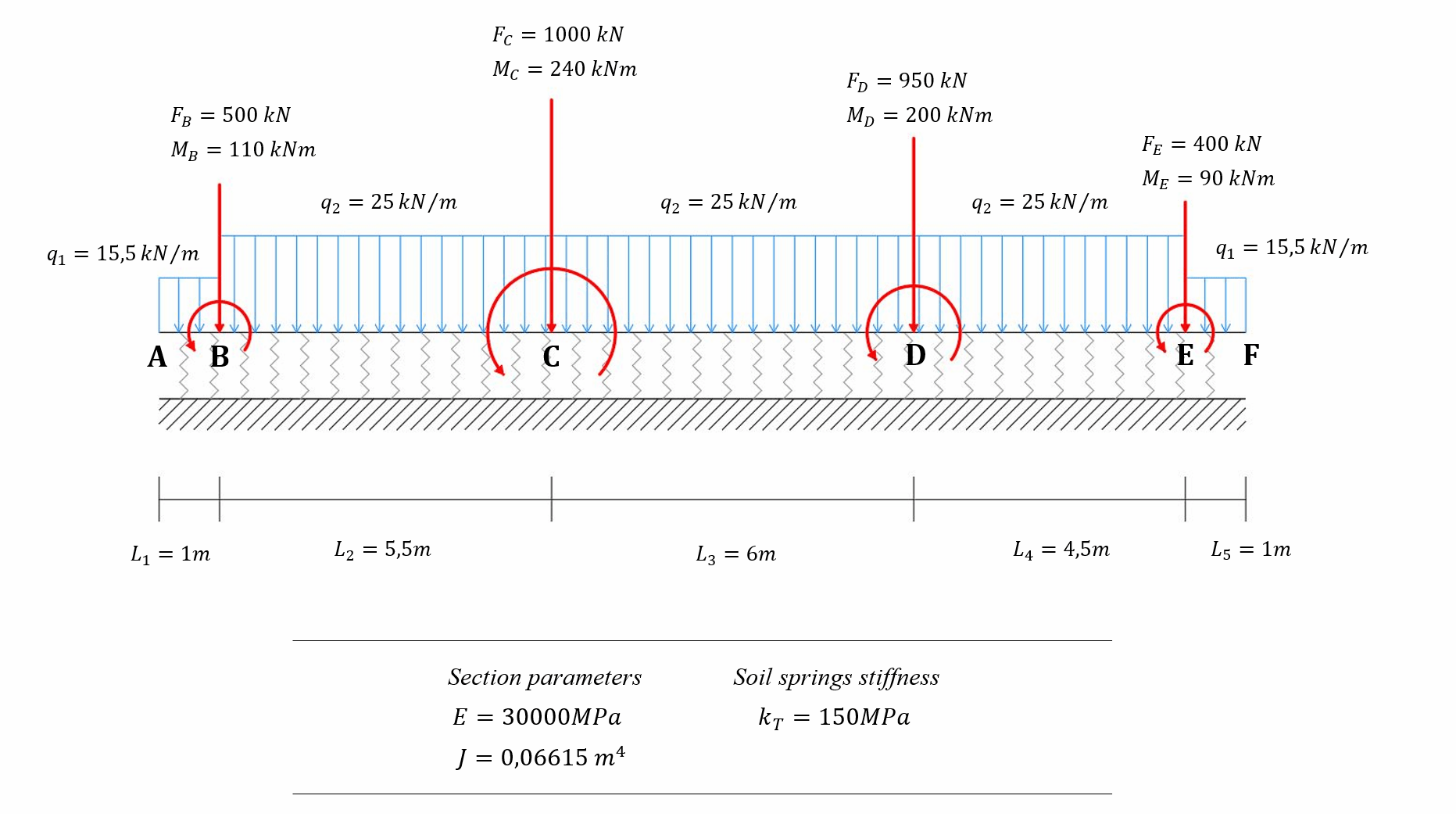
Il modello è stato costruito e risolto con WeStatiX. Se volete imparare a creare un modello di trave Winkler, date un’occhiata a questo e ad altri esempi e tutorial.
Dopo aver modellato la geometria della trave, sono stati applicati i carichi distribuiti e nodali. Il supporto Winkler è stato inserito applicando i vincoli dei membri elastici. In questo modo, una volta eseguita la discretizzazione della trave, il codice ha applicato il vincolo nodale con la rigidità 
In particolare, il diagramma degli spostamenti verticali:
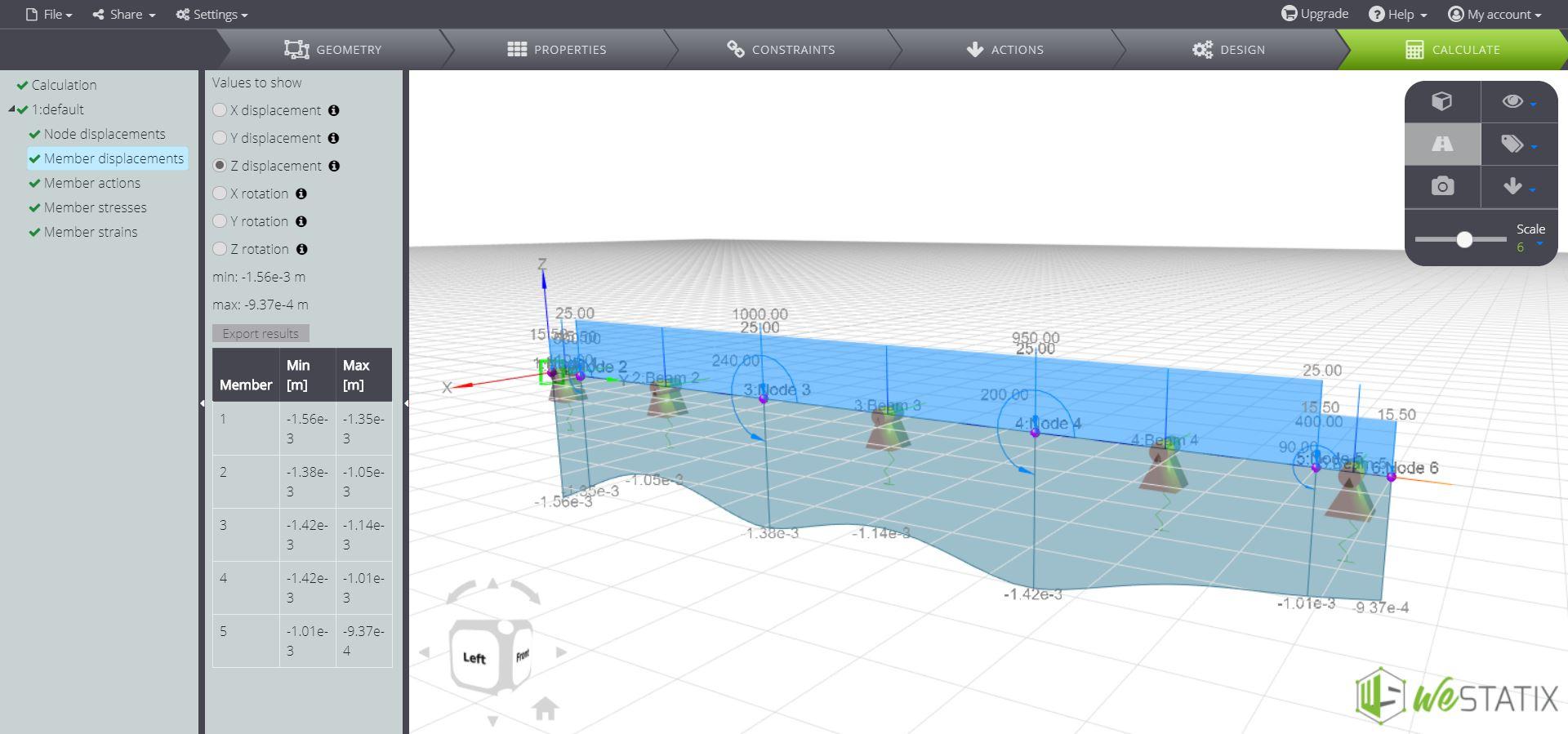
Si può notare che lo spostamento verticale non è costante, ma presenta dei picchi la cui intensità può essere valutata con precisione utilizzando questa strategia di modellazione.
Il diagramma della forza di taglio:
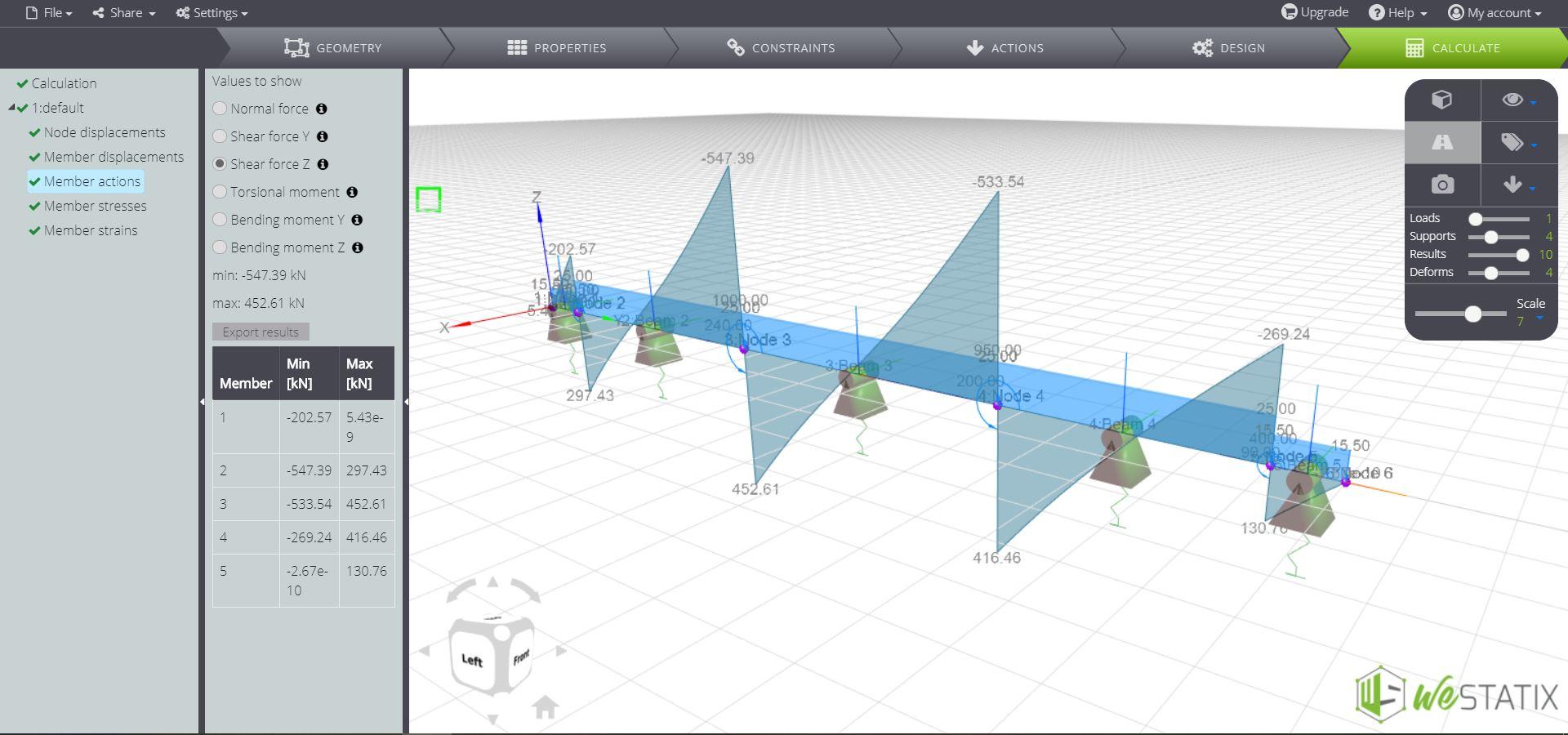
Il diagramma del momento flettente:
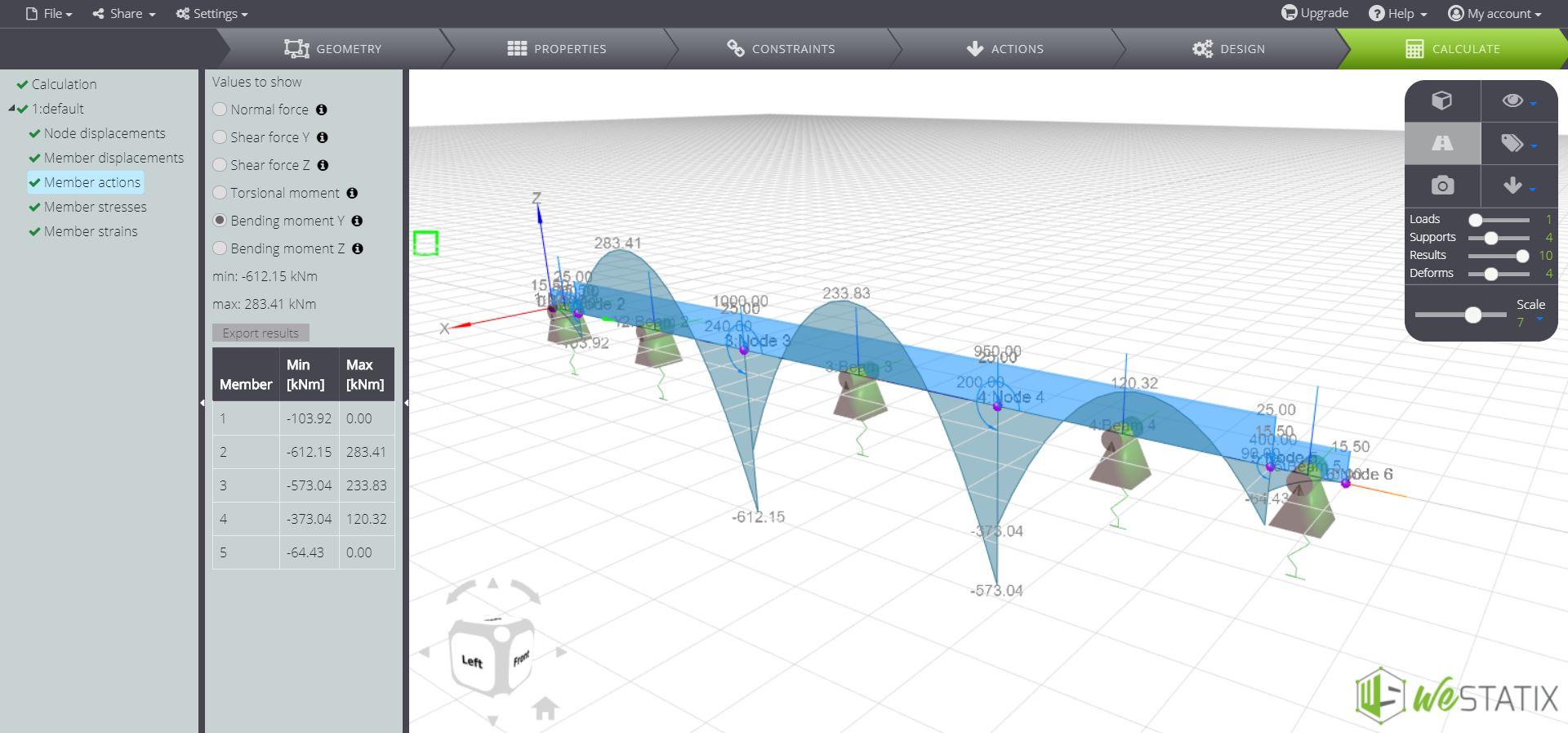
Conoscendo l’esatta distribuzione delle azioni di taglio e flessione nella trave, si possono adottare scelte progettuali corrette ed evitare inutili sovradimensionamenti. Inoltre, è possibile eseguire diversi calcoli per valutare la risposta strutturale considerando l’incertezza nella rigidità del terreno, ottenendo così un inviluppo di valori di azione per la trave di fondazione.
I risultati ottenuti coincidono con le soluzioni analitiche presentate in [1]. È possibile verificare l’accuratezza della soluzione WeStatiX dando un’occhiata al test di validazione dei supporti Winkler.
In WeStatiX potete trovare altre applicazioni dei vincoli elastici! Ad esempio, volete imparare a modellare fondazioni profonde su supporti elastici o una pavimentazione industriale realizzata con calcestruzzo fibrorinforzato? Queste e altre applicazioni sono disponibili sul sito
WeStatiX
.
Riferimenti
[1] Colajanni P., Falsone G., Recupero A., Formulazione semplificata della soluzione per travi su fondazione Winkler che ammette discontinuità dovute a carichi e vincoli, International Journal for Engineering Education, 25, 1, 75 – 83, (2009).
